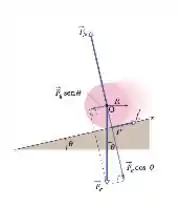
A figura mostra um disco homogêneo de raio rolando para baixo sem deslizar, com velocidade angular variável, em uma rampa inclinada em um ângulo . As forças que estão atuando nele são as forças peso , a força normal e a força de atrito . O ponto está no centro de massa do disco. É possível afirmar que:
- Nenhuma das forças mostradas realiza torque em relação ao ponto O.
- A energia cinética do disco é puramente translacional.
- A energia cinética total do disco é dada por , onde é seu momento de inércia em relação ao eixo que passa pelo ponto perpendicularmente ao plano do disco.
- A velocidade linear do ponto do disco em contato com o plano (ponto P na figura) é
- O torque resultante em relação ao ponto é não nulo e é realizado apenas por .
- A condição de rolamento sem deslizamento é que o torque resultante em relação ao ponto O seja nulo.
- A condição de rolamento sem deslizamento é que a aceleração do ponto O seja .
Passo 1
Aqui devemos analisar três coisas e resolvemos todas as alternativas:
1°- O torque realizado.
2°- A energia Cinética nesse caso.
3°- Condição para rolamento sem deslizamento.
Passo 2
O torque realizado nada mais nada menos é do que :
O que a gente vê é que o torque depende do tamanho da força , da distância até o centro de massa, e o ângulo que a força faz com o vetor distância.
A força Peso e a normal agem no centro de massa (pode olhar na figura), logo elas não realizam torque. A única força que não está no centro de massa é a força de atrito , que gera um torque de . Fazendo o disco girar.
Assim a gente já mataria de cara a questão, dizendo que a letra e está correta.
Mas vamos provar que as outras estão erradas
Passo 3
Energia Cinética
Ele tá transladando (movendo seu centro de massa) e rotacionando, certo?
Então, para o ato de transladar, temos uma parcela de energia cinética de translação e para o ato de rotacionar, a gente vai ter outra parcela, a energia cinética de rotação
Logo:
Ouxe! Aí a a gente já eliminava a letra b e c.
Passo 4
Condição para rolamento sem deslizamento:
Para rolar sem deslizar, devemos ter que no ponto de contato entre o disco e a base a velocidade linear é zero. ( d falsa)
A aceleração não pode ser calculada por . Essa aceleração é a chamada aceleração centrípeta, se ela estivesse ocorrendo o corpo somente iria rotacionar, e não transladar, pois faltaria a componente tangencial. Entendeu?
Daí a gente já mata letra g.
Letra f. Se não houver torque, o corpo nem irá rotacionar. Logo, não tem como ser um rolamento sem deslizamento.
Resposta
Letra e