Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Movimento Circular Acelerado

Ver Teoria
Exercício 521234567891011121314151617181920212223242526272829303132333435363738394041424344454647484950515354555657

Enunciado

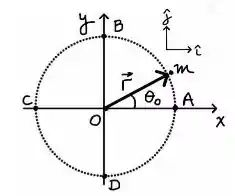
Uma partícula de massa m está na ponta de uma haste fina que pode girar em torno de um eixo fixo perpendicular ao plano x y , passando por sua origem. A partícula pode descrever um movimento circular (linha pontilhada) descrito pelo ângulo θ com o eixo x , orientado positivamente no sentido anti-horário. No instante t = 0 , a partícula encontra-se parada em θ = θ 0 > 0 (vide figura), quando a haste começa a se mover com aceleração angular constante α > 0 .

Seja a → = a x   i ^ + a y j ^ o vetor aceleração de m , onde i ^ e j ^   são os vetores unitários nas direções x   e   y , respectivamente. Quando a partícula passa pelo ponto A pela primeira vez a x e a y satisfazem:

  1. a x > 0 e a y > 0
  2. a x > 0 e a y = 0
  3. a x > 0 e a y < 0
  4. a x < 0 e a y > 0
  5. a x < 0 e a y = 0
  6. a x < 0 e a y < 0
  7. a x = 0 e a y > 0
  8. a x = 0 e a y = 0
  9. a x = 0 e a y < 0

Passo 1

Tá massa! Saquei!

Ele falou aqui que a partícula (no desenho vou colocar uma sombrinha de frevo :D) está rodando com um uma aceleração angular positiva ( α > 0 ). Isso quer nos dizer que ele está fazendo um movimento circular (aceleração centrípeta), porém com o aumento do módulo da velocidade (aceleração tangencial).

Se ligou?

Passo 2

A aceleração centrípeta aponta sempre para o centro, e a tangencial aponta tangente a curva, e como α > 0 está na direção do movimento!

Show de bola! Como ele nos pediu o vetor no ponto A, teremos a figura abaixo:

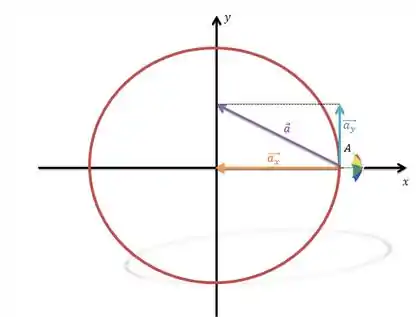
- i ^ ) e a aceleração tangencial positiva na direção j ^ .

Já viu qual a certa? Só marcar lá!

Simbora passar, esse(a) menino(a)!

Resposta

Letra d

Exercícios de Livros Relacionados

O volante de uma máquina a vapor gira com uma velocidade angular constante de 150r e v / m i n . Quando a máquina é desligada, o atrito dos mancais e a resistência do ar param a roda em2,2h . (a) Qual
O prato de um toca-discos está girando a 33 1 3r e v / m i n . Uma semente de melancia está sobre o prato a 6,0c m de distância do eixo de rotação. (a) Calcule a aceleração da semente, supondo que ela
Na Figura 9.38 , o cilindro e a polia giram sem atrito em torno de um eixo horizontal fixo que passa pelos seus centros. Uma corda leve é enrolada em volta do cilindro, passa sobre a polia e possui um
Um roda começa a girar a partir do repouso em t= 0 com aceleração angular constante. No instante t=2,0s , a velocidade angular da roda é 5,0r a d / s . A aceleração cessa abruptamente no instante t=20
Um carro parte do repouso e se move em uma pista circular com 30,0m de raio . A velocidade do carro aumenta a uma taxa constante de 0 , 500m / s 2 . (a) Qual é o módulo da aceleração linear média do c