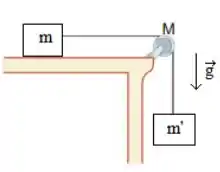
Considere o sistema mostrado na figura abaixo. A massa , que desliza sem atrito, está ligada à massa suspensa pelo fio que passa sem deslizar sobre uma polia homongênea de massa e raio . A polia gira sem atrito sobre um eixo horizontal, perpendicular ao plano da polia, que passa por seu centro de massa. A aceleração da gravidade é dada por e o momento de inércia da polia em relação ao eixo mencionado vale . A aceleração da massa , em termos de , , e é:
Passo 1
Bora lá, pessoal! Essa questão já é bem manjada e tal! Então vale a pena você ficar seguro pra resolvê-la pois a probabilidade dela cair na sua prova é bem alta!
Foca aí!
O primeiro passo na hora de resolver essas questõezinhas é isolar as forças nos dois blocos e na polia! Saca só:
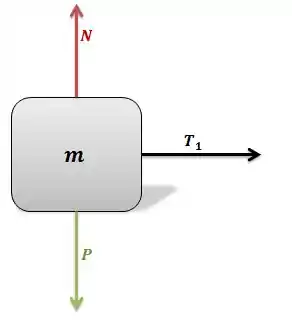
Para o bloco de massa , teremos:
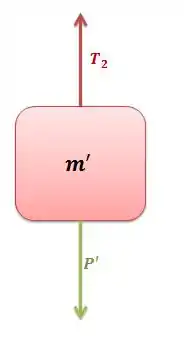
Para o bloco de massa , vai ficar:
Já pra polia, a gente vai ter:
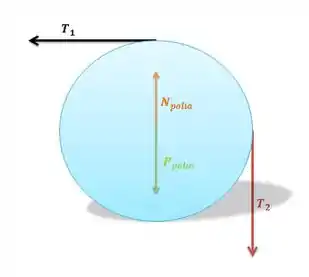
Mas véi, pera aí! E essas duas forças aí no meio?
Assim, no fim das contas ela não vai mudar nada nas suas contas. Elas só mostram que a polia está fixa, não translada devido àquele pino.
Passo 2
Beleza! Próximo passo é escrever as equações da 2ª Lei de Newton para cada um.
Bloco :
Como ele só é arrastado na direção horizontal, podemos só considerar a equação em , que será:
Bloco :
Como ele só é puxado na direção vertical, podemos considerar só a equação em , logo a gente vai ter:
(Nesse caso coloquei como sendo positivo as forças apontando para baixo).
Bloco :
Aqui vamos aplicar a Segunda Lei de Newton para rotação, que no caso é dada por:
Passo 3
O torque por sua vez pode ser calculado pelas forças que as trações fazem nele, certo?
Mas véi, como você definiu quem era positivo ou negativo?
Coloquei como positivo o torque a favor do movimento, no caso resiste contra o movimento o movimento do bloco descer. Deu pra entender?
Passo 4
Se liga que ele deu o nosso .
E o , sabemos que ele vem da relação:
Logo:
Assim...
Passo 5
Agora, é só pegar os valores de e lá do passo .
Isolando o vai ficar:
:D~
Resposta
Letra a