3º EE de Física 1 da UFPE - 2017.2

Uma barra delgada de massa e comprimento é mantida na vertical com uma das extremidades apoiada no solo e depois é liberada. A extremidade superior atinge o solo sem que a extremidade de apoio deslize. Utilize que .

Julgue as seguintes assertivas.

A energia mecânica do sistema se conserva durante a queda, pois a força peso é conservativa.

A energia mecânica da barra não se conserva durante a queda, pois como a barra não desliza existe a ação de uma força de atrito diferente de zero.

O módulo do deslocamento vertical do centro de massa da barra entre o instante inicial e o instante em que a barra toca o solo é .

É correto apenas o que se afirma em:

(a)

(b)

(c)

(d) e

(e) e

(f) e

(g) Todas

(h) Nenhuma

Uma polia com momento de inércia em relação ao eixo e raio é submetida a uma força aplicada tangencialmente à sua borda de módulo com em Newtons e em segundos. Admitindo que a polia está inicialmente em repouso, determine a velocidade angular da polia no instante .

(a)

(b)

(c)

(d)

(e)

(f)

(g)

(h)

(i)

Uma barra delgada de massa e comprimento é mantida na vertical com uma das extremidades apoiada no solo e depois é liberada. A extremidade superior atinge o solo sem que a extremidade de apoio deslize. Utilize que .

A velocidade da extremidade superior da barra imediatamente antes de tocar o solo é:

(a)

(b)

(c)

(d)

(e)

(f)

(g)

(h)

(i)

Uma barra homogênea de comprimento e massa está inicialmente em repouso. A barra pode girar sem atrito em torno de um eixo que passa em sua extremidade superior e é perpendicular ao plano da página, conforme a figura ao lado. Uma partícula de massa colide horizontalmente com a barra a uma velocidade e a uma distância do eixo de rotação. A colisão é perfeitamente inelástica e a partícula fica presa à barra após a colisão.

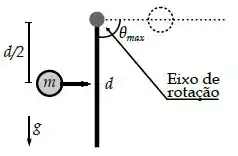
Dados: , momento de inércia de uma barra em torno de um eixo que passa pelo centro de massa .

(a) Qual é o momento de inércia do conjunto partícula+barra em relação ao eixo de rotação no instante imediatamente após a colisão?

(b) Após a colisão, a energia mecânica do sistema é conservada e verifica-se que o conjunto partícula+barra atinge um ângulo máximo . Obtenha a velocidade angular do conjunto imediatamente após a colisão.

(c) Supondo que a colisão entre a partícula e a barra ocorre durante um tempo infinitesimal, determine a velocidade do partícula imediatamente antes da colisão.

Uma roda homogênea de massa e raio encontra-se inicialmente em repouso sobre uma superfície horizontal (ver figura abaixo). O plano da roda é vertical. A partir de um instante de tempo aplica-se uma força horizontal constante de módulo no seu centro, e a roda passa a girar sem deslizar.

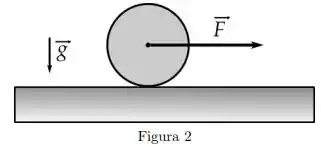
Nesse caso, a força de atrito entre a roda e a superfície:

é nula e a energia total da roda é conservada.

é diferente de zero e a energia total da roda não é conservada.

é diferente de zero e a energia total da roda é conservada.

é diferente de zero e é estática.

é diferente de zero e é cinética.

é igual ao coeficiente de atrito multiplicado pelo módulo da força normal.

Estão corretas somente as afirmações:

(a)

(b) e

(c) , e

(d) e

(e) , e

(f) e

(g) , e

(h) e

(i) , e

Uma caixa encontra-se sobre um carrossel, a uma distância do eixo de rotação. Inicialmente todo o sistema encontra-se em repouso. No instante o motor do carrossel é ligado e sua velocidade angular aumenta linearmente com o tempo, até atingir um valor máximo no instante , conforme mostrado na figura. Depois disso, a velocidade angular permanece constante neste valor máximo. Suponha que a caixa não escorregue em nenhum momento.

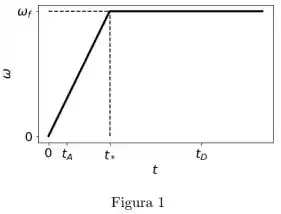
Suponha, agora, que em a caixa esteja na iminência de escorregar. Se , e , qual é o valor do coeficiente de atrito estático entre a caixa e o carrossel?

(a)

(b)

(c)

(d)

(e)

(f)

(g)

(h)

Uma caixa encontra-se sobre um carrossel, a uma distância do eixo de rotação. Inicialmente todo o sistema encontra-se em repouso. No instante o motor do carrossel é ligado e sua velocidade angular aumenta linearmente com o tempo, até atingir um valor máximo no instante , conforme mostrado na figura. Depois disso, a velocidade angular permanece constante neste valor máximo. Suponha que a caixa não escorregue em nenhum momento.

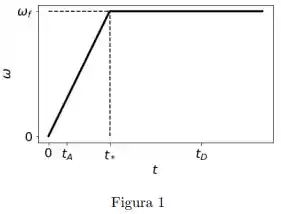
Considere os instantes de tempo e mostrados na figura e analise as seguintes afirmações:

() A aceleração tangencial da caixa em é não nula.

() A aceleração centrípeta da caixa em é não nula.

() A aceleração tangencial da caixa em é não nula.

Das afirmações acima, são verdadeiras apenas:

(a)

(b)

(c)

(d) e

(e) e

(f) e

(g) Todas

(h) Nenhuma

Uma roda homogênea de massa e raio encontra-se inicialmente em repouso sobre uma superfície horizontal (ver figura abaixo). O plano da roda é vertical. A partir de um instante de tempo aplica-se uma força horizontal constante de módulo no seu centro, e a roda passa a girar sem deslizar.

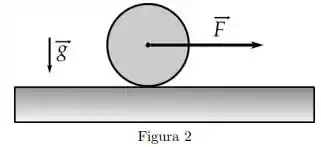
Sabe-se que o momento de inércia da roda em relação ao seu eixo de rotação é . Denotando a aceleração do seu centro de massa por , pode-se afirmar que:

(a)

(b)

(c)

(d)

(e)

(f)

(g)