Uma roda homogênea de massa e raio encontra-se inicialmente em repouso sobre uma superfície horizontal (ver figura abaixo). O plano da roda é vertical. A partir de um instante de tempo aplica-se uma força horizontal constante de módulo no seu centro, e a roda passa a girar sem deslizar.
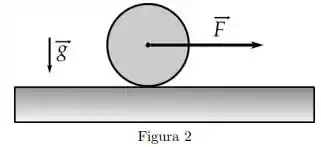
Sabe-se que o momento de inércia da roda em relação ao seu eixo de rotação é . Denotando a aceleração do seu centro de massa por , pode-se afirmar que:
(a)
(b)
(c)
(d)
(e)
(f)
(g)
Passo 1
Para encontrar isso, vamos escrever as duas equações de movimento do disco.
Translação:
Rotação:
E além disso, como o disco rola sem deslizar, sua aceleração do centro de massa e sua aceleração angular estão relacionados por:
Juntando essas três equações conseguimos resolver o problema.
Passo 2
Quem são as forças sobre a roda?
Na direção do movimento temos a força e a força de atrito :
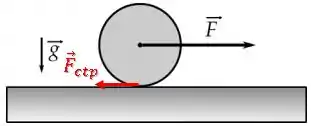
Então para a translação, temos:
Passo 3
Agora, vamos escrever a quação para a rotação.
O torque resultante será a soma dos torques de cada uma das forças atuando sobre o disco.
Além das forças e , temos também uma força peso e uma força normal , que são perpendiculares ao movimento.
As forças e estão aplicadas no centro de massa do disco, então não geram torque.
A força está na direção passando pelo centro de massa do disco, então, ela também não gera torque.
A única que gera torque é a força , dado por:
Então, temos:
Substituindo o valor do momento de inércia:
Cortando :
Passo 4
Ficamos com esse sisteminha aqui:
Como queremos que a expressão final de tenha em vez de , vamos substituir o da segunda equação usando a relação:
Então:
Substituindo o valor de na primeira equação, temos:
Resposta
Letra (d)