Uma roda homogênea de massa e raio encontra-se inicialmente em repouso sobre uma superfície horizontal (ver figura abaixo). O plano da roda é vertical. A partir de um instante de tempo aplica-se uma força horizontal constante de módulo no seu centro, e a roda passa a girar sem deslizar.

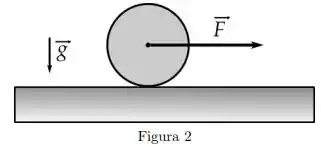
Nesse caso, a força de atrito entre a roda e a superfície:

é nula e a energia total da roda é conservada.

é diferente de zero e a energia total da roda não é conservada.

é diferente de zero e a energia total da roda é conservada.

é diferente de zero e é estática.

é diferente de zero e é cinética.

é igual ao coeficiente de atrito multiplicado pelo módulo da força normal.

Estão corretas somente as afirmações:

(a)

(b) e

(c) , e

(d) e

(e) , e

(f) e

(g) , e

(h) e

(i) , e

Como é essa força de atrito?

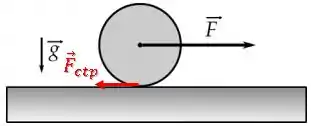
Ela aponta para a esquerda, pois a tendência de deslizamento da roda é para a direita.

Além disso, como não há deslizamento, o ponto de contato com o chão está parado. Assim, a força de atrito será estática.

Então, A afirmativa está correta e a afirmativa está incorreta.

Entretanto, não podemos garantir que essa força de atrito estático é máxima...

Isso vai depender tanto do valor da força quanto da geometria e massa (momento de inércia) da roda.

Então, ela não necessariamente vale . Portanto, a afirmativa está incorreta.

Faltam as afirmativas , .

A energia total se conserva?

Aqui existe uma certa ambiguidade na afirmativa...

A energia total do sistema na verdade está aumentando, uma vez que a roda está ganhando velocidade a partir da aceleração resultante.

Entretanto, como a força de atrito é estática, seu trabalho é nulo:

Então, por mais que exista uma força de atrito, esse atrito é estático e não retira energia do sistema.

Logo, toda a energia adquirida pela roda permanecerá na roda. A energia se conserva, por mais que ela não seja a mesma a cada instante.

A afirmativa está correta e a afirmativa está incorreta.

Então, as afirmativas corretas são e . Ficamos com a alternativa (f).