Uma caixa encontra-se sobre um carrossel, a uma distância do eixo de rotação. Inicialmente todo o sistema encontra-se em repouso. No instante o motor do carrossel é ligado e sua velocidade angular aumenta linearmente com o tempo, até atingir um valor máximo no instante , conforme mostrado na figura. Depois disso, a velocidade angular permanece constante neste valor máximo. Suponha que a caixa não escorregue em nenhum momento.
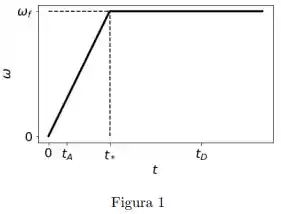
Considere os instantes de tempo e mostrados na figura e analise as seguintes afirmações:
() A aceleração tangencial da caixa em é não nula.
() A aceleração centrípeta da caixa em é não nula.
() A aceleração tangencial da caixa em é não nula.
Das afirmações acima, são verdadeiras apenas:
(a)
(b)
(c)
(d) e
(e) e
(f) e
(g) Todas
(h) Nenhuma
Passo 1
Lá vamos nós com o famoso carrossel das questões de física.
Mas essa aqui é rapidinha! Se liga na situação...
Quando o carrosel está parado , não há nem força centrípeta nem força tangencial:
Passo 2
No trecho entre e , o carrosel começa a girar acelerado.
Então, como a caixa realiza uma trajetória circular, há uma componente de força centrípeta.
Porém, além da centrípeta, temos uma componente de força tangencial, pois o movimento circular é acelerado pelo motor:
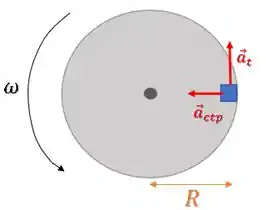
Então em , temos tanto aceleração tangencial quanto centrípeta.
As afirmativas e estão corretas.
Passo 3
Já no trecho a partir de , o carrossel passa a girar com velocidade angular constante.
Assim, o movimento da caixa será um movimento circular uniforme. Logo, a força resultante na caixa será uma força apontando para o centro da trajetória, força centrípeta:
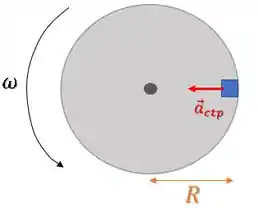
Então, em temos apenas força centrípeta. A aceleração tangencial é nula.
A afirmativa está incorreta.
Ficamos com a alternativa (d).
Resposta
Letra (d)