Uma barra homogênea de comprimento e massa está inicialmente em repouso. A barra pode girar sem atrito em torno de um eixo que passa em sua extremidade superior e é perpendicular ao plano da página, conforme a figura ao lado. Uma partícula de massa colide horizontalmente com a barra a uma velocidade e a uma distância do eixo de rotação. A colisão é perfeitamente inelástica e a partícula fica presa à barra após a colisão.
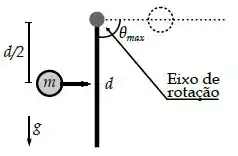
Dados: , momento de inércia de uma barra em torno de um eixo que passa pelo centro de massa .
(a) Qual é o momento de inércia do conjunto partícula+barra em relação ao eixo de rotação no instante imediatamente após a colisão?
(b) Após a colisão, a energia mecânica do sistema é conservada e verifica-se que o conjunto partícula+barra atinge um ângulo máximo . Obtenha a velocidade angular do conjunto imediatamente após a colisão.
(c) Supondo que a colisão entre a partícula e a barra ocorre durante um tempo infinitesimal, determine a velocidade do partícula imediatamente antes da colisão.
Passo 1
Na letra (a), queremos o momento de inércia do conjunto partícula+barra.
O momento de inércia do conjunto será a soma do momento de inércia da partícula com o momento de inércia da barra , ambos com relação ao eixo de rotação:
Passo 2
O momento de inércia de uma partícula é dado por:
A partícula colide com a barra à uma distância igual à metade do comprimento da barra, então:
Passo 3
O momento de inércia de uma barra com relação a um eixo perpendicular passando pelo seu centro é:
Entretanto, nosso eixo de rotação não está passando pelo centro da barra, ele está passando pela extremidade. Então, vamos usar o teorema dos eixos paralelos para achar esse momento de inércia:
Sendo a distância entre os eixos igual à metade do comprimento da barra:
Passo 4
Assim, achamos o momento de inércia do conjunto:
Substituindo os valores, temos:
Passo 5
Na letra (b), queremos a velocidade angular imediatamente após a colisão, considerando que a energia mecânica do sistema se conserva.
O próprio enunciado já entregou o caminho...
Vamos usar a conservação da energia mecânica:
Considerando que na situação inicial a energia potencial gravitacional é nula, teremos apenas a energia cinética de rotação do conjunto:
Enquanto na situação final temos apenas energia potencial gravitacional já que a barra se encontra parada:
A altura será a altura do centro de massa na situação final com relçao à situação inicial:
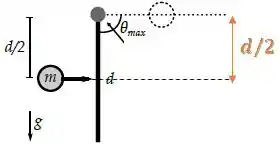
Então:
Passo 6
Voltando à conservação da energia, temos:
Substituindo os valores:
Passo 7
Na letra (c), queremos a velocidade da partícula imediatamente antes da colisão.
Geralmente quando temos uma colisão entre partículas, acabamos usando a conservação do momento linear, porém, nesse caso a barra está presa por um eixo que exerce força sobre o conjunto. Assim, o momento linear não se conserva.
Porém, podemos pensar em algo similar para rotações... o momento angular.
Como a barra gira em torno do eixo, essa força não exerce torque sobre o sistema, logo o momento angular se conserva:
Com essa equação, conseguimos a velocidade da partícula antes da colisão que aparece em .
Passo 8
Inicialmente, apenas a partícula se mexe, logo o momento angular do sistema será dado pelo momento angular de uma partícula:
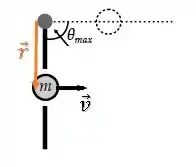
Como esses vetores são perpendiculares, temos que o módulo do momento angular é:
Já o momento angular final será dado pela expressão do conjunto em rotação:
Passo 9
Voltando à nossa expressão, temos:
Substituindo os valores, temos:
Resposta
(a)
(b)
(c)