PF de Física 1 da UFPE - 2016.1

Uma partícula se desloca ao longo do eixo sob a ação de uma força cuja componente é dada por:

Onde está em metros. O trabalho realizado pela força quando a partícula se desloca da origem até é igual a:

A figura abaixo mostra uma chapa retangular, de comprimento e largura , que pode girar sem atrito em torno de um eixo perpendicular à figura que passa por um de seus vértices (ponto ). Duas forças e , cujos módulos são iguais a e independem do tempo , são aplicadas ao sistema paralelamente às arestas da chapa, conforme mostra a figura. Em a chapa se encontra em repouso.

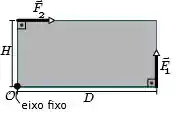
Com respeito ao módulo do momento angular da chapa em relação a O, pode-se afirmar que:

(a)

(b)

(c)

(d)

(e)

(f)

(g)

(h)

Um objeto se move ao longo do eixo sob a ação de uma forca conservativa. A energia potencial associada a essa força é mostrada na figura ao lado. Sabe-se que é um ponto de retorno. Se é a energia cinética do sistema em e é a componente da forca ao longo da trajetória do objeto no trecho , assinale a alternativa correta:

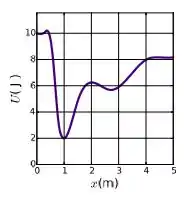
(a)

(b)

(c)

(d)

(e)

(f)

(g)

(h)

(i)

Uma nave espacial de massa viaja com velocidade constante pelo espaço, sem interagir com qualquer outro corpo celeste. Num dado instante, ela explode, partindo-se em dois pedaços. O primeiro pedaço, de massa , passa a deslocar-se com velocidade constante. O segundo pedaço, de massa , passa a deslocar-se com velocidade constante . Todas as respostas abaixo devem ser escritas em termos de e .

(a) Calcule o vetor velocidade (expresso em termos dos vetores unitários e ).

(b) Qual é a velocidade do centro de massa do sistema após a explosão? Calcule ou justifique sua resposta.

(c) Calcule a variação da energia mecânica devida à explosão.

Uma casca esférica de massa e raio é abandonada em repouso na beirada de um hemisfério de raio , deslizando sem escorregar, como mostra a figura. Considere a aceleração gravitacional local . Quando a esfera passa pelo ponto mais baixo do hemisfério, calcule:

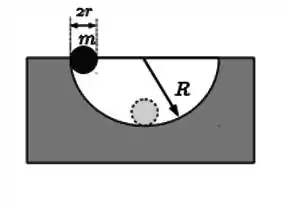
(a) Os módulos das velocidades angular da esfera e do centro de massa da esfera.

(b) A fração da energia cinética total correspondente à energia cinética de rotação.

(c) A forca exercida pela esfera sobre o hemisfério, expressa em termos de .

Dado: o momento de inércia de uma casca esférica de massa e raio em relação a um eixo que passa por um de seus diâmetros é .

Parte de uma ferrovia é composta por dois trechos retilíneos mutuamente ortogonais conectados por um arco de circunferência conforme mostrado na figura abaixo. Uma locomotiva percorre a ferrovia no sentido do ponto ao ponto com velocidade de módulo constante.

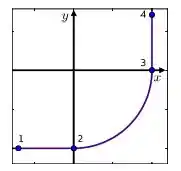
Considere, então, os trechos abaixo, em que o tempo é representado no eixo horizontal, enquanto no eixo vertical encontra-se alguma função de . Assinale a alternativa que lista corretamente os trechos correspondentes à componente da velocidade, à componente da velocidade, ao módulo da aceleração e à aceleração tangencial, respectivamente, da locomotiva em função de :

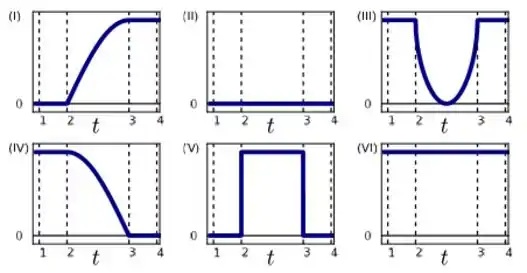
(a)

(b)

(c)

(d)

(e)

(f)

(g)

(h)