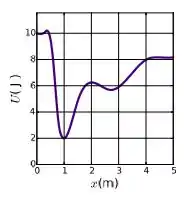
Um objeto se move ao longo do eixo sob a ação de uma forca conservativa. A energia potencial associada a essa força é mostrada na figura ao lado. Sabe-se que é um ponto de retorno. Se é a energia cinética do sistema em e é a componente da forca ao longo da trajetória do objeto no trecho , assinale a alternativa correta:
(a)
(b)
(c)
(d)
(e)
(f)
(g)
(h)
(i)
Passo 1
Você lembra o que significa um ponto de retorno? Não? Vamos lembrar então.
Um ponto de retorno é aquele cuja energia cinética é nula, ou seja, a energia potencial é máxima.
Portanto, analisando nosso problema, temos que, no ponto , temos:
e
Onde é a energia cinética no ponto e é a energia potencial.
Já no ponto , temos que:
e
Como a força do problema é conservativa, a energia mecânica se conserva, portanto:
Logo:
Passo 2
Já para sabermos informações sobre a força, temos a seguinte relação:
Lembra como analisa a derivada em um gráfico? Você pega um ponto e analisa a inclinação da função naquele ponto. Se for crescente, a derivada é positiva, se for decrescente, é negativa. Beleza?
Então vamos lá! Dá uma olhada no gráfico entre os pontos e . A curva está subindo né? Portanto, por conta do sinal de menos:
O que nos dá como resposta a letra (b)
Resposta
Letra (b)