Uma casca esférica de massa e raio é abandonada em repouso na beirada de um hemisfério de raio , deslizando sem escorregar, como mostra a figura. Considere a aceleração gravitacional local . Quando a esfera passa pelo ponto mais baixo do hemisfério, calcule:
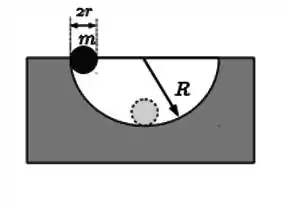
(a) Os módulos das velocidades angular da esfera e do centro de massa da esfera.
(b) A fração da energia cinética total correspondente à energia cinética de rotação.
(c) A forca exercida pela esfera sobre o hemisfério, expressa em termos de .
Dado: o momento de inércia de uma casca esférica de massa e raio em relação a um eixo que passa por um de seus diâmetros é .
Passo 1
a) Como a força de atrito não realiza trabalho em um rolamento sem deslizamento, temos que a energia mecânica se conserva. Se é a velocidade angular do centro de massa no ponto mais baixo da trajetória, temos que, também neste ponto:
Se fizermos então a conservação da energia mecânica, tudo em relação ao centro de massa da casca:
Isolando :
Já para calcular o
Passo 2
b) Para calcular essa razão, temos que:
E:
Logo:
Portanto, a energia cinética de rotação contribui com para a energia cinética total.
Passo 3
No ponto mais baixo da trajetória, sabemos que a força resultante que aponta para cima deve ser igual a força centrípeta.
No entanto, lembre-se que o raio da trajetória não é , e sim , já que estamos considerando o centro de massa da casca.
Portanto:
Da letra (a), sabemos que:
Portanto:
Resposta
a) e
b)
c)