A figura abaixo mostra uma chapa retangular, de comprimento e largura , que pode girar sem atrito em torno de um eixo perpendicular à figura que passa por um de seus vértices (ponto ). Duas forças e , cujos módulos são iguais a e independem do tempo , são aplicadas ao sistema paralelamente às arestas da chapa, conforme mostra a figura. Em a chapa se encontra em repouso.
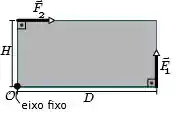
Com respeito ao módulo do momento angular da chapa em relação a O, pode-se afirmar que:
(a)
(b)
(c)
(d)
(e)
(f)
(g)
(h)
Passo 1
Aqui nós temos que lembrar da relação entre o torque e o momento angular. Lembra? Se liga:
Com isso, temos que calcular o torque aplicado na placa. Sem mistérios, vamos lá:
Usando a regra da mão direita para o produto vetorial, e já tirando o módulo do torque:
Substituindo os valores:
Passo 2
Agora precisamos encontrar o momento angular!
Integrando:
Como é constante com o tempo:
Logo:
Nos dando como resposta a letra (d)
Resposta
Letra (d)