PF de Física 1 da UFPE - 2017.2

Um eixo é espetado no centro de massa de uma garrafa, perpendicularmente ao comprimento. Nesta situação, o momento de inércia medido experimentalmente é . Quando o eixo é deslocado paralelamente para um ponto O, a uma distância de do centro de massa, o momento de inércia medido é . A massa da garrafa é:

(a)

(b)

(c)

(d)

(e)

(f)

(g)

(h)

Um bloco encontra-se na iminência de deslizamento sobre um plano inclinado que forma um ângulo com a horizontal. Qual é o valor do coeficiente de atrito estático ?

(a)

(b)

(c)

(d)

(e)

(f)

(g)

(h)

O vetor velocidade (em ) de uma partícula é , onde e são os vetores unitários ao longo dos eixos e , respectivamente. Em que instante a partícula inverte o sentido do seu movimento?

(a)

(b)

(c)

(d)

(e)

(f)

(g)

(h)

Um bloco de massa desliza em uma superfície sem atrito e explode em dois fragmentos de massas e . A velocidade do bloco antes da explosão era e o momento linear do fragmento 1 após a explosão é . O módulo da velocidade do fragmento 2 após a explosão é:

(a)

(b)

(c)

(d)

(e)

(f)

(g)

(h)

(i)

Um corpo de massa move-se ao longo do eixo preso a uma mola de constante elástica . A mola fica relaxada quando o corpo está na posição . A velocidade do corpo em é de no sentido positivo do eixo . Qual é sua velocidade quando ele passa por ?

(a)

(b)

(c)

(d)

(e)

(f)

(g)

(h)

(i)

Um bloco é puxado por uma distância horizontal ao longo de uma superfície com atrito por uma força constante que faz um ângulo com a horizontal, conforme a figura abaixo. Sabe-se que o módulo da força aplicada é . Considere que o bloco não perde contato com a superfície em nenhum momento.

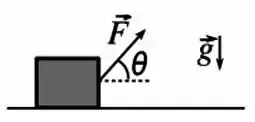
(a) Determine o trabalho realizado pela força quando .

(b) Calcule o trabalho realizado pela força quando .

(c) Qual é o trabalho realizado pela força peso quando ? Justifique.

Um disco homogêneo gira ao redor de um eixo de rotação que passa no seu centro e é perpendicular à sua superfície. O seu momento de inércia em relação ao eixo de rotação é . A posição angular (em ) de um ponto no disco é dada por , onde o tempo é dado em segundos. O torque resultante no disco em relação ao seu centro no instante vale:

(a)

(b)

(c)

(d)

(e)

(f)

(g)

(h)

(i)