O vetor velocidade (em ) de uma partícula é , onde e são os vetores unitários ao longo dos eixos e , respectivamente. Em que instante a partícula inverte o sentido do seu movimento?
(a)
(b)
(c)
(d)
(e)
(f)
(g)
(h)
Passo 1
Imagina um carro andando para a direita mas com uma aceleração no sentido contrário...
Sua velocidade irá diminuir até que em um dado momento ela troque de sentido.
Que instante será esse?
Será o instante em que a velocidade dele é zero:
Ah beleza, então para um corpo inverter o sentido de seu movimento, sua velocidade deve passar pelo zero.
Para a partícula dessa questão temos a mesma situação, porém em duas dimensões. Então, vamos achar o instante em que essa velocidade vale zero ao longo dos dois eixos.
Passo 2
Vamos começar com :
Esse é o gráfico da velocidade em função do tempo:
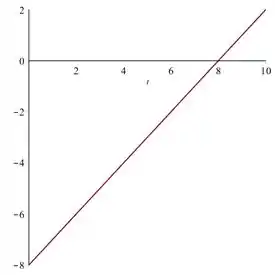
Podemos ver que a velocidade começa negativa em passa a ser positiva, logo a partícula inverte seu movimento ao longo desse eixo.
Passo 3
Agora vamos ao eixo .
Temos duas raízes:
Repara que achamos o mesmo instante em que troca de sentido...
Esse é o gráfico da velocidade em funão do tempo:
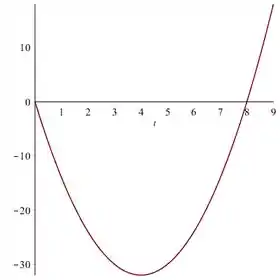
Podemos ver que a velocidade passa de negativa a positiva em , logo a partícula inverte seu movimento ao longo do eixo .
Então em a partícula troca de sentido tanto ao longo do eixo quanto ao longo do eixo , então podemos dizer que ela inverte o sentido de seu movimento.
Resposta
Letra (h)