Um bloco é puxado por uma distância horizontal ao longo de uma superfície com atrito por uma força constante que faz um ângulo com a horizontal, conforme a figura abaixo. Sabe-se que o módulo da força aplicada é . Considere que o bloco não perde contato com a superfície em nenhum momento.
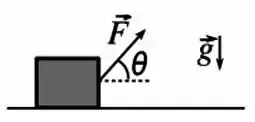
(a) Determine o trabalho realizado pela força quando .
(b) Calcule o trabalho realizado pela força quando .
(c) Qual é o trabalho realizado pela força peso quando ? Justifique.
Passo 1
Sabemos que o deslocamento do bloco é horizontal, enquanto a força está inclinada em um ângulo com a horizontal:
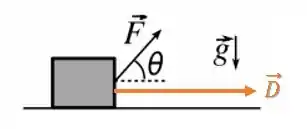
O trabalho da força será o produto escalar entre o vetor força e o vetor deslocamento :
Esse produto escalar pode ser calculado a partir dos módulos dos vetores vezes o cosseno do ângulo entre eles:
Qual é a ideia aqui?
A ideia é que quanto menor o ângulo entre a força e o deslocamento (mais próximo de estarem na mesma direção), maior será o trabalho , pois o cosseno se aproxima de .
Enquanto isso, quanto mais próximo de estiver o ângulo (vetores próximos de serem perpendiculares), menor será o trabalho , pois o cosseno se aproxima de .
Isso é o mesmo que decompor a força ...
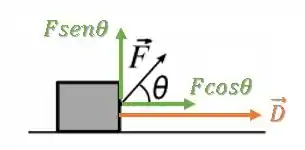
... e dizer que a componente (perpendicular) não realiza trabalho e a componente (mesma direção) realiza trabalho, dado pelo produto dos módulos (mesma direção).
Passo 2
Na letra (a), queremos quando .
O trabalho é dado pelo produto escalar:
Como , temos:
Isso faz sentido com o que já vimos... o trabalho de uma força na mesma direção do deslocamento é o produto dos módulos.
Substituindo os valores, temos:
Passo 3
Na letra (b), queremos quando .
Faremos o mesmo procedimento...
Como , temos:
Substituindo os valores, temos:
OBS: O trabalho nesse caso tem que ser menor que no item (a), já que a força está inclinada com relação ao deslocamento.
Passo 4
Na letra (c), queremos o trabalho da força peso quando .
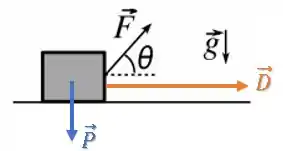
O trabalho da força peso será:
Sendo o ângulo entre eles.
Como o deslocamento é horizontal e a força peso vertical, esse ângulo é:
Assim, o trabalho é:
Como , temos:
O trabalho de uma força perpendicular ao deslocamento é nulo.
Também poderíamos pensar que como não há variação de altura do bloco (deslocamento horizontal), o trabalho do força peso é nulo.
Resposta
(a)
(b)
(c)