P2 de Física 1 da UFRJ - 2016.2

Uma patinadora está girando em torno de um eixo vertical que passa pelo seu centro de massa. Inicialmente, ela está com os seus braços abertos e gira com uma velocidade angular constante . Depois ela aproxima os braços do corpo e a velocidade angular passa a ser . Quais das alternativas que se seguem estão corretas?

(I) O momento de inércia da patinadora com os braços abertos é maior que seu momento de inércia com os braços fechados.

(II) A velocidade angular é menor que a velocidade angular

(III) O momento angular do sistema quando a patinadora está de braços abertos é igual aquele quando ela fecha os braços.

a) todas estão corretas

b) apenas (I)

c) apenas (II)

d) apenas (III)

e) apenas (I) e (II)

f) apenas (I) e (III)

g) apenas (II) e (III)

h) nenhuma está correta

Das partículas e , com a mesma massa, descrevem circunferências concêntricas de raios e , respectivamente, sendo . Os sentidos de giro das partículas são opostos, com velocidades de mesmo módulo. Quais das afirmativas que seguem são corretas?

(I) Os momentos angulares das duas partículas em relação ao centro das trajetórias têm mesmos direção e sentido.

(II) O módulo do momento angular do sistema formado pelas duas partículas em relação ao centro das trajetórias é nulo.

(III) O momento linear do sistema formado pelas duas partículas é sempre nulo.

a) nenhuma está correta

b) apenas (I)

c) apenas (III)

d) apenas (I) e (II)

e) apenas (II) e (III)

f) apenas (I) e (III)

g) todas estão corretas

h) apenas (II)

Um disco homogêneo de massa e raio pode girar livremente em torno de um eixo perpendicular a ele que passa pelo seu CM, cujo momento de inércia é . O disco parte do repouso e inicia uma subida sobre a rampa, ao ter seu eixo puxado por uma força constante de módulo , paralela à superfície da rampa, como indica a figura. A superfície da rampa está inclinada de um ângulo com a horizontal e o disco rola sem deslizar ao subir por essa superfície. Nas questões abaixo indique claramente os conceitos utilizados.

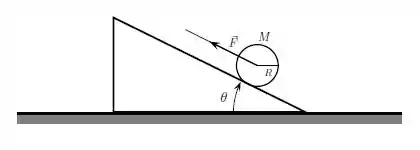
a) Faça um diagrama indicando as forças que atuam no disco.

b) Determine o módulo da aceleração do centro de massa, , do disco.

c) Determine o tempo que ele leva para completar a primeira volta em torno do seu eixo em função de e dos dados do problema.

d) Determine o trabalho realizado por cada uma das forças indicadas no item (a) na primeira volta completa em torno de seu eixo, justificando cada uma delas.

Um sapo está, inicialmente, situado num dos extremos de uma plataforma de comprimento que flutua, em repouso, sobre as águas paradas de um lago. Num dado instante, o sapo dá um salto com uma velocidade de módulo e que faz com a horizontal um ângulo como mostra a figura. Suponha que a plataforma se movimente apenas na horizontal e despreze o atrito entre a água e a plataforma. Seja a massa do sapo e a massa da plataforma. Após o sapo pular, pode-se afirmar que:

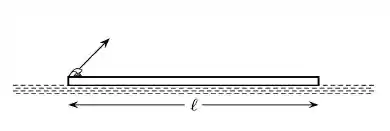
a) a plataforma se move para esquerda com velocidade de módulo

b) a plataforma se move para esquerda com velocidade de módulo

c) a plataforma se move para direita com velocidade de módulo

d) a plataforma se move para esquerda com velocidade de módulo

e) a plataforma se move para esquerda com velocidade de módulo

f) a plataforma não se move

Dois pequenos discos (que podem ser considerados como partículas), de massa e , se deslocam sobre uma mesa horizontal, sem atrito, conforme mostra a figura abaixo. Inicialmente eles possuem velocidades em direções perpendiculares de mesmo módulo . Num certo instante, ocorre uma colisão e o sistema passa a se deslocar em conjunto a partir desse momento. As respostas dos itens abaixo devem ser dadas em função de e .

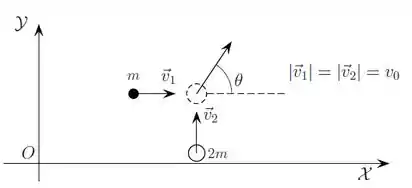
a) Calcule o módulo de , que é a velocidade depois que os discos se movimentam juntos e o ângulo que esse vetor faz com o eixo . Indique qual(quais) Lei(s) de conservação está(ão) sendo utilizada(s) e o porquê.

b) Calcule a variação da energia cinética entre os instantes anterior e posterior à colisão.

c) Calcule o vetor velocidade do centro de massa do sistema antes de ocorrer a colisão.

Considere duas barras finas, homogêneas, de comprimento e massa . Ambas têm um de seus pontos presos a um suporte no teto de maneira que podem girar, livremente, em torno desse ponto. Uma delas (I) está presa por uma de suas extremidades enquanto a outra (II) está presa a um ponto localizado a uma distância de uma de suas extremidades. Considere que a barra I é abandonada do repouso, quando se encontra na horizontal e a barra II é lançada, a partir da posição horizontal, com uma velocidade angular diferente de zero, de maneira que ambas chegam na posição vertical com mesma velocidade angular . Sobre a energia cinética e o módulo do torque resultante em relação ao ponto fixo de cada barra quando elas passam pela posição vertical, é correto afirmar que:

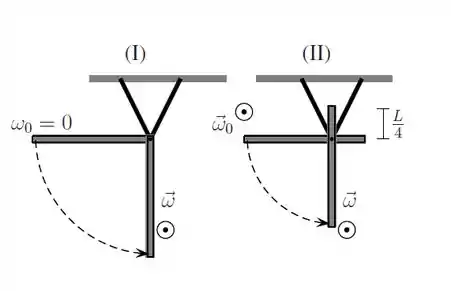
a) e

b) e

c) e

d) e

e) e

f) e

Uma bola de bilhar recebe uma tacada como indicada na figura. O atrito entra a bola e a mesa é desprezível. Imediatamente após a tacada, pode-se afirmar que:

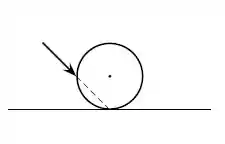
a) a bola se desloca para direita e gira no sentido anti-horário

b) a bola se desloca para esquerda e gira no sentido horário

c) a bola se desloca para direita e gira no sentido horário

d) a bola se desloca para esquerda e gira no sentido anti-horário

e) a bola se desloca para direita e não gira

Em um experimento de colisão nuclear, mediu-se o espalhamento de partículas , de massa e velocidade inicial , após elas colidirem com núcleos de ouro em repouso e de massa . Sabe-se que as forças externas são desprezíveis. Se a velocidade da partícula medida após a colisão é , pode-se afirmar que:

a) a velocidade do núcleo de ouro após a colisão é

b) a velocidade do núcleo de ouro após a colisão é

c) a velocidade do núcleo de ouro após a colisão é

d) a velocidade do núcleo de ouro após a colisão é

e) a velocidade do núcleo de ouro após a colisão é