Um disco homogêneo de massa e raio pode girar livremente em torno de um eixo perpendicular a ele que passa pelo seu CM, cujo momento de inércia é . O disco parte do repouso e inicia uma subida sobre a rampa, ao ter seu eixo puxado por uma força constante de módulo , paralela à superfície da rampa, como indica a figura. A superfície da rampa está inclinada de um ângulo com a horizontal e o disco rola sem deslizar ao subir por essa superfície. Nas questões abaixo indique claramente os conceitos utilizados.
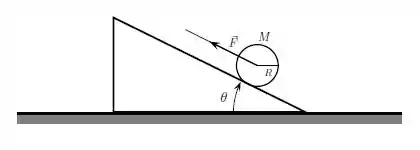
a) Faça um diagrama indicando as forças que atuam no disco.
b) Determine o módulo da aceleração do centro de massa, , do disco.
c) Determine o tempo que ele leva para completar a primeira volta em torno do seu eixo em função de e dos dados do problema.
d) Determine o trabalho realizado por cada uma das forças indicadas no item (a) na primeira volta completa em torno de seu eixo, justificando cada uma delas.
Passo 1
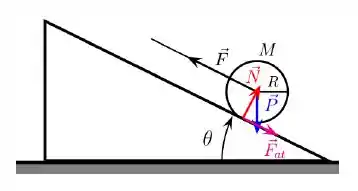
a) Aqui não podemos esquecer da força de atrito, porque é ela a responsável por realizar o rolamento do disco. Sem ela, só haveria deslizamento.
Atente também para o sentido da força de atrito. Se o disco fosse arrastado sem rolamento, o deslocamento da superfície seria para cima, certo? Portanto a força de atrito aponta para baixo, para contrariar esse movimento.
Passo 2
b) Usando a segunda lei de Newton, temos:
Para a componente paralela ao plano inclinado, temos:
Passo 3
Nessa expressão tem uma força que nós não conhecemos, que é a força de atrito. Para isso vamos lançar mão de mais uma expressão conhecida, a do torque:
Dado que a força de atrito é a única força cuja linha de ação não passa pelo eixo de rotação, ela é a única que produz torque, então:
Sabemos que:
E:
Substituindo:
Passo 4
Substituindo na equação inicial:
Isolando a aceleração:
Passo 5
c) Como o centro de massa seguiu um MRUV, temos que encontrar o tempo que demora para o disco percorrer uma distância igual a , certo? Usando a expressão do MRUV:
Passo 6
d) Esta alternativa é meio complicadinha, mas vamos lá. Você tem que perceber que tanto a normal quanto a força de atrito são aplicadas sobre o “Centro Instantâneo de Rotação”, que, em todos os instantes do movimento está em repouso e, portanto, não deixa que essas forças realizem trabalho.
Já a força peso realiza trabalho que, por definição, é a variação da energia potencial gravitacional.
Como o disco andou na direção do plano uma distância , a diferença de altura desses dois pontos é:
E o trabalho do peso:
A força também realiza trabalho, mas como ela está na direção do movimento, é mais fácil de calcular:
Resposta
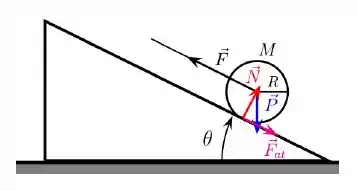
a)
b)
c)
d)