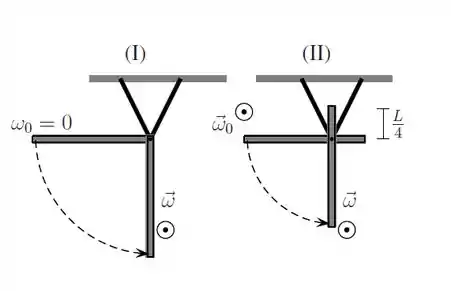
Considere duas barras finas, homogêneas, de comprimento e massa . Ambas têm um de seus pontos presos a um suporte no teto de maneira que podem girar, livremente, em torno desse ponto. Uma delas (I) está presa por uma de suas extremidades enquanto a outra (II) está presa a um ponto localizado a uma distância de uma de suas extremidades. Considere que a barra I é abandonada do repouso, quando se encontra na horizontal e a barra II é lançada, a partir da posição horizontal, com uma velocidade angular diferente de zero, de maneira que ambas chegam na posição vertical com mesma velocidade angular . Sobre a energia cinética e o módulo do torque resultante em relação ao ponto fixo de cada barra quando elas passam pela posição vertical, é correto afirmar que:
a) e
b) e
c) e
d) e
e) e
f) e
Passo 1
Primeiro temos que analisar qual é a diferença causada por uma barra estar presa na extremidade e outra a da extremidade. Vocês já tem uma desconfiança? Sim, a principal mudança nesses dois casos é o momento de inércia.
Sabemos que para uma barra presa na extremidade, temos:
Já para a haste II, temos que usar o teorema dos eixos paralelos:
Passo 2
Sabemos que a energia cinética de rotação é dada por:
Como nos foi dito que a velocidade angular é a mesma para as duas hastes quando estas chegam na posição vertical e como , temos que:
Passo 3
Sabemos que o torque só é diferente de zero se a força que estiver agindo no corpo estiver em uma linha de ação que não passe pelo eixo de rotação, certo?
No nosso caso, quando as barras estão na vertical, a única força agindo nelas é o peso e a normal com o pino, e as duas passam pelo eixo de rotação, portanto:
Resposta
(a)