Dois pequenos discos (que podem ser considerados como partículas), de massa e , se deslocam sobre uma mesa horizontal, sem atrito, conforme mostra a figura abaixo. Inicialmente eles possuem velocidades em direções perpendiculares de mesmo módulo . Num certo instante, ocorre uma colisão e o sistema passa a se deslocar em conjunto a partir desse momento. As respostas dos itens abaixo devem ser dadas em função de e .
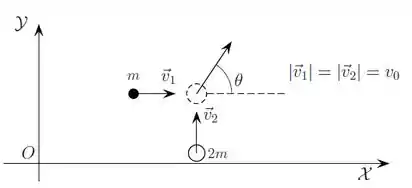
a) Calcule o módulo de , que é a velocidade depois que os discos se movimentam juntos e o ângulo que esse vetor faz com o eixo . Indique qual(quais) Lei(s) de conservação está(ão) sendo utilizada(s) e o porquê.
b) Calcule a variação da energia cinética entre os instantes anterior e posterior à colisão.
c) Calcule o vetor velocidade do centro de massa do sistema antes de ocorrer a colisão.
Passo 1
a) A única força atuante nos discos é o peso, que é anulado pela normal, portanto, podemos usar a conservação do momento linear:
Passo 2
Sabemos que antes do choque, temos:
E depois do choque, temos que os discos se unem e adquirem velocidade :
Passo 3
Utilizando a conservação:
Portanto:
Geometricamente também temos que:
Passo 4
b) Podemos achar a variação da energia cinética da seguinte maneira:
Passo 5
c) Dado que o momento linear se conserva, o vetor velocidade do centro de massa também se conserva, logo:
Resposta
a) e
b)
c)