P2 de Física 1 da UFRJ - 2017.1

Considere um sistema formado por duas pequenas esferas de massas e , ligadas por uma mola ideal. Inicialmente, a mola é comprimida e o sistema é lançado, liberando a mola, de uma certa altura acima do solo, com o centro de massa tendo velocidade na direção horizontal e as esferas tendo uma velocidade angular , em relação à posição do centro de massa. Sobre o movimento que se segue é correto afirmar que:

(a) A posição do centro de massa do sistema descreverá uma trajetória parabólica, de um projétil.

(b) As esferas executarão um movimento circular uniforme em torno da posição do centro de massa, de velocidade angular .

(c) Ambas as esferas vão descrever um movimento parabólico, de projétil.

(d) A esfera de massa vai realizar um movimento circular uniforme em torno da esfera de massa .

(e) No instante imediatamente anterior ao sistema atingir o solo, necessariamente a esfera de massa terá uma velocidade angular em torno da posição do centro de massa de , onde é a distância entre a esfera e a posição do CM.

Um disco que girava em torno de seu eixo de simetria com velocidade angular constante começa a ser freado com desaceleração angular uniforme até atingir o repouso. No processo em que ele é freado ele completa exatamente uma volta de seu movimento.

Um outro disco, idêntico ao primeiro, mas que possui velocidade angular inicial começa a ser freado com mesma desaceleração angular que o primeiro. Quantas voltas completas em torno de seu eixo esse segundo disco dá até atingir o repouso?

(a) 25

(b) 10

(c) 5

(d) 2

(e) 1

Uma patinadora no gelo executa sua apresentação e começa a girar de braços abertos, com uma certa velocidade angular. Ao fechar os braços, qual das quantidades, relacionadas à patinadora, �� conservada?

(a) Momento angular em relação a seu eixo de rotação.

(b) Momento de inércia em relação a seu eixo de rotação.

(c) Velocidade angular de rotação.

(d) Energia cinética de rotação.

Uma pequena esfera de massa desliza ao longo do eixo x em uma mesa horizontal sem atrito e colide elasticamente, frontalmente, com uma outra esfera, de massa > , que estava inicialmente em repouso (a colisão é unidimensional). O gráfico abaixo mostra a posição da esfera de massa em função do tempo até o instante da colisão , que ocorre na posição (linha sólida). Qual a reta tracejada indicada no gráfico que representa a evolução da posição da esfera de massa m após a colisão?

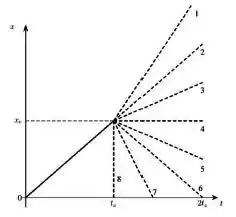
1. 5
2. 1
3. 2
4. 3
5. 4
6. 6
7. 7
8. 8

Uma partícula de massa desloca-se sobre uma mesa horizontal, sem atrito, com velocidade de módulo . Num certo instante ela se desintegra espontaneamente em três fragmentos de massas , e como mostrado na figura. O módulo da velocidade do fragmento de massa é igual àquele de massa , ao passo que o fragmento de massa segue a mesma direção e sentido da velocidade original da partícula.

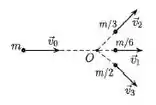
Qual das quantidades associadas ao sistema de massa a seguir não se conserva no processo de desintegração?

(a) Energia cinética.

(b) Momento linear.

(c) Velocidade da posição do centro de massa.

(d) Momento angular em relação ao ponto O, onde ocorreu a desintegração.

(e) Massa total.

Uma esfera rola sem deslizar por uma superfície horizontal de maneira que a velocidade de seu centro de massa é constante . A figura mostra duas vistas da situação: à esquerda uma vista do alto da mesa e à direita uma vista por trás da esfera.

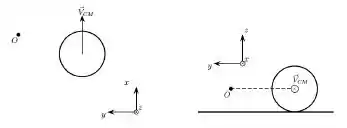
Em relação ao ponto O, indicado na figura, que está a mesma altura da posição do centro de massa da esfera, no sistema de eixos também indicado na figura, é correto afirmar que o momento angular da esfera tem componentes não nulas:

(a) .

(b) Apenas .

(c) Apenas .

(d) Apenas .

(e)

(f)

(g) Todas as 3 componentes.

Uma barra fina rígida, de comprimento e massa distribuída de maneira uniforme ao longo de seu comprimento, está sobre uma mesa horizontal sem atrito, e pode girar em torno de uma de suas extremidades, que está fixada à mesa. Em um determinado instante, são aplicadas três forças à barra . Conforme mostra a figura abaixo, são aplicadas no meio da barra, enquanto é aplicada na extremidade oposta à fixa. As forças são perpendiculares à barra enquanto faz um ângulo , tal que .

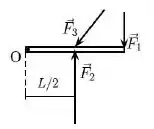
Sobre os módulos dos torques causados por cada uma das forças, em relação ao ponto fixo (O), é válida a relação:

(a) |

(b)

(c)

(d)

(e)

Considere um corpo rígido constituído por hastes rígidas sem massa e de comprimento e um conjunto de nove esferas de mesma massa (que podem ser consideradas partículas). O sistema pode ser colocado para girar em torno de 3 eixos, indicados na figura: o eixo AB, o eixo CD e o eixo z, que é perpendicular ao plano definido pelo corpo rígido e passa pela esfera do canto inferior direito.

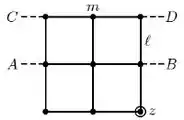
Sabendo que pode-se fornecer sempre a mesma energia de rotação ao corpo rígido, qual a relação entre os módulos das velocidades angulares de rotação em cada um dos 3 casos?

(a

(b

(c)

(d)

(e)

Uma esfera rígida homogênea de raio rola sem deslizar sobre uma superfície horizontal com velocidade angular constante e velocidade do centro de massa . A figura mostra quatro pontos na superfície da esfera contidos no plano vertical da velocidade . Considere , , e os vetores velocidade dos pontos 1, 2, 3 e 4, respectivamente.

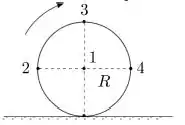
A resposta correta é:

(a)

(b)

(c)

(d)

(e)

(f)

Um carretel é composto por um cilindro interno de raio e massa , enrolado por um fio ideal, com 2 discos idênticos, de massa e raio cada um, por fora do cilindro interno, concêntricos a este último (como um iô-iô). Inicialmente o carretel está em repouso em uma superfície horizontal quando o fio enrolado ao cilindro interno começa a ser puxado na direção horizontal, conforme a figura, por uma força de módulo . Observa-se que o cilindro rola sem

deslizar sobre a superfície horizontal e sabe-se que o momento de inércia de um cilindro de massa m e raio r′ em relação a um eixo que passa por seu eixo desimetria é .

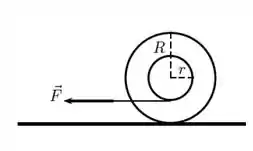
Indique as respostas em termos de .

(a) Mostre que o momento de inércia do carretel, em relação a seu eixo de simetria, vale

(b) Qual a direção e o sentido da força de atrito que atua no carretel?

(c) Determine o módulo e o sentido da aceleração do centro de massa do carretel.

(d) Qual a velocidade angular de rotação do carretel, em torno do eixo de simetria

que passa por seu centro de massa, após ele completar uma volta depois do instante

em que a força começa a atuar?

(e) Determine a energia cinética associada ao carretel no instante em que ele completa

a primeira volta após o início da aplicação da força .