Uma barra fina rígida, de comprimento e massa distribuída de maneira uniforme ao longo de seu comprimento, está sobre uma mesa horizontal sem atrito, e pode girar em torno de uma de suas extremidades, que está fixada à mesa. Em um determinado instante, são aplicadas três forças à barra . Conforme mostra a figura abaixo, são aplicadas no meio da barra, enquanto é aplicada na extremidade oposta à fixa. As forças são perpendiculares à barra enquanto faz um ângulo , tal que .
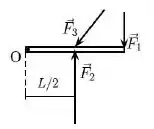
Sobre os módulos dos torques causados por cada uma das forças, em relação ao ponto fixo (O), é válida a relação:
(a) |
(b)
(c)
(d)
(e)
Passo 1
Sendo o torque calculado como:
Onde é o ângulo com a horizontal e a distância do ponto de aplicação da forço ao ponto fixo.
Para facilitar, chamaremos de . Consequentemente, .
Calculando o torque para cada um, teremos:
Para :
Para :
Para :
Como . Logo, podemos afirmar que para , o termo será multiplicado por um valor menor que 1. Assim: