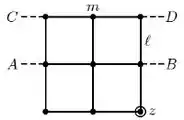
Considere um corpo rígido constituído por hastes rígidas sem massa e de comprimento e um conjunto de nove esferas de mesma massa (que podem ser consideradas partículas). O sistema pode ser colocado para girar em torno de 3 eixos, indicados na figura: o eixo AB, o eixo CD e o eixo z, que é perpendicular ao plano definido pelo corpo rígido e passa pela esfera do canto inferior direito.

Sabendo que pode-se fornecer sempre a mesma energia de rotação ao corpo rígido, qual a relação entre os módulos das velocidades angulares de rotação em cada um dos 3 casos?

(a

(b

(c)

(d)

(e)

Sabendo que a energia de rotação é calculada de acordo com a seguinte relação:

E de acordo com o enunciado, o valor da energia é o mesmo para todos os casos, podemos concluir que quanto maior o momento de inércia, menor a velocidade angular e quando menor o momento de inércia, maior a velocidade angular. Então, calcularemos o momento de inércia para cada um dos casos.

Sabendo que para cada esfera o momento de inércia é calculado por:

Onde é a massa da esfera e a distância da esfera ao eixo, podemos calcular o momento de inércia do conjunto.

Rotação em torno do eixo AB:

Rotação em torno do eixo CD:

Rotação em torno do eixo z:

Como:

Logo,