PF de Física 1 da UFRJ - 2014.1

Duas partículas e de massas iguais colidem unidimensionalmente ao longo do eixo . Os gráficos a seguir representam as velocidades em função do tempo para cada partícula. Se é o momento linear do sistema formado pelas duas partículas e sua energia cinética, podemos afirmar que nessa colisão

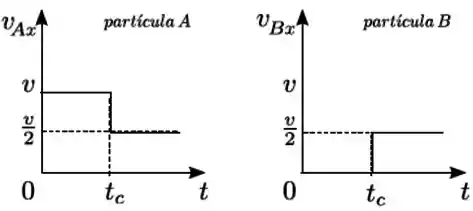
(a) se conserva e não se conserva

(b) se conserva e se conserva

(c) não se conserva e não se conserva

(d) não se conserva e se conserva

(e) e

Três partículas de massas iguais a movem-se na ausência de forças externas com velocidades e . Num dado instante elas ocupam as posições indicadas na figura abaixo. O vetor momento angular total deste sistema de partículas em relação a origem do eixo de coordenadas da figura é

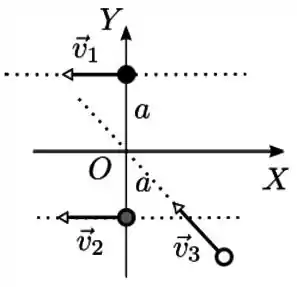
(a)

(b)

(c)

(d)

(e)

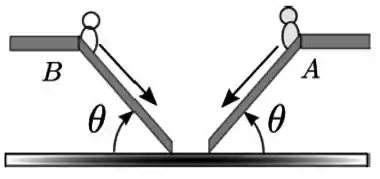
Duas escadas rolantes estão dispostas como mostra a figura. O ângulo de elevação de cada escada, em relação a horizontal é o mesmo. As escadas movimentam os degraus com velocidades constantes de mesmo módulo , medidas em relação a um referencial fixo na Terra. Em um dado instante, duas pessoas e entram simultaneamente nas escadas, como mostra a figura, e ao entrarem permanecem paradas em relação aos respectivos degraus. Seja um referencial fixo em e em translação relativa ao referencial da Terra. O módulo da velocidade de em relação enquanto e estão nas escadas é

(a)

(b)

(c) não é constante

(d)

(e)

Dois blocos de massas e estão ligados por um fio ideal que passa por uma roldana homogênea, também de massa , e de raio . A roldana é sustentada por um eixo horizontal coincidente com seu eixo geométrico de simetria, como ilustra a figura. Não há atrito entre o eixo e a roldana e o fio não desliza sobre ela. Considere o intervalo de tempo com um instante inicial em que a roldana e os blocos estão em repouso e um instante final em que o bloco mais pesado já desceu uma distância vertical .

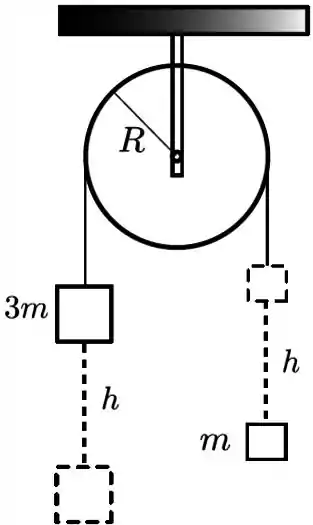
Considere como dados e o módulo da aceleração da gravidade. O momento de inércia da roldana relativo ao seu eixo de simetria é . Calcule

a) a variação da energia cinética do sistema constituído pela roldana e os blocos no intervalo de tempo considerado;

b) o módulo da velocidade do bloco mais pesado no instante final;

c) a razão entre a energia cinética de rotação da roldana e a energia cinética total de translação dos dois blocos no instante final.

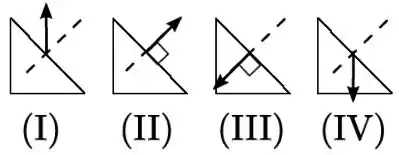
Um bloco de massa está sobre uma mesa horizontal sendo empurrado em movimento retilíneo por uma força constante dada, com velocidade e aceleração de mesmo sentido que a força; o coeficiente de atrito cinético entre o bloco e a mesa é . Sobre esse primeiro bloco há um segundo bloco de mesma massa e rigidamente colado ao primeiro, como indica a figura.

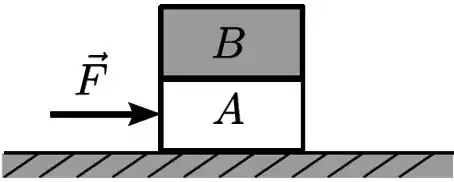
a) Faça um diagrama de forças externas sobre o sistema constituído pelos dois blocos;

b) Calcule o módulo a da aceleração com a qual os blocos se deslocam;

c) Calcule os módulos da força horizontal e da força vertical que o bloco exerce sobre o bloco .

Dois discos de massas e estão ligados por uma barra rígida de massa sobre uma mesa horizontal lisa. Uma força paralela ao plano da mesa está aplicada sobre o primeiro disco em um certo instante, como mostra a figura (da mesa vista de cima). Nesse instante, a aceleração do centro de massa do sistema constituído pelos discos e pela barra

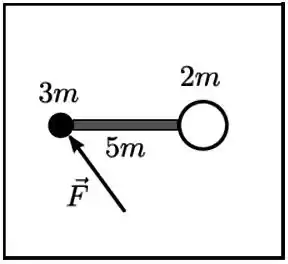
(a)

(b)

(c)

(d)

(e)

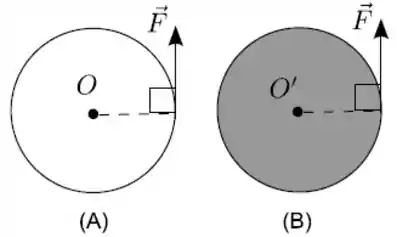
Dois discos e de mesmo raio , constituídos de materiais homogêneos, repousam sobre uma mesa horizontal lisa. Aplica-se a mesma forca a cada disco, tangencialmente às suas respectivas periferias, como indica a figura, fazendo-os girar em torno de um pino central no disco e no disco .

Considerando a massa do disco maior do que a massa do disco , as relações entre os módulos dos torques e , em relação a e , devido À força e os módulos das respectivas acelerações angulares resultantes e são dadas por

(a) e

(b) e

(c) e

(d) e

(e) e

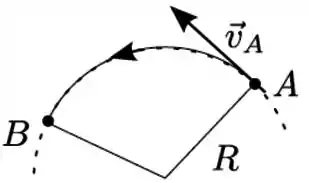
Uma partícula percorre uma trajetória circular de raio onde, no trecho do arco , o módulo da sua velocidade é reduzido uniformemente, isto é, com derivada constante. No ponto a sua velocidade é , conforme ilustrado na figura. Considere a sua aceleração decomposta segundo duas direções, um componente na direção radial (aceleração radial) e o outro componente na direção tangente à trajetória (aceleração tangencial). No seu movimento de para a afirmativa correta é

(a) a aceleração tem módulo constante;

(b) a aceleração radial tem módulo constante;

(c) a aceleração tangencial tem módulo constante;

(d) a aceleração tangencial é sempre nula;

(e) nenhuma das respostas anteriores.

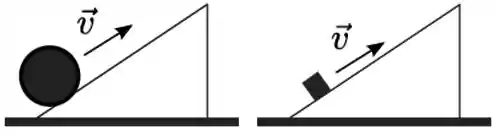
Uma esfera é lançada rolando sem deslizar subindo um plano inclinado com velocidade inicial do seu centro de massa. Um bloco é lançado subindo em translação um plano inclinado com a mesma inclinação e com a mesma velocidade inicial do seu centro de massa. No plano onde se encontra a esfera há atrito suficiente para que ela permaneça rolando sem deslizar e no plano onde está o bloco não há atrito.

A relação entre a altura máxima que o bloco atinge e a altura máxima que a esfera atinge nos respectivos planos é dada por

(a) , pois tanto a energia cinética do bloco como a da esfera se conserva.

(b) , pois tanto a energia mecânica do bloco como a da esfera se conserva.

(c) , pois o bloco desliza sem atrito.

(d) , pois a esfera rola sem deslizar.

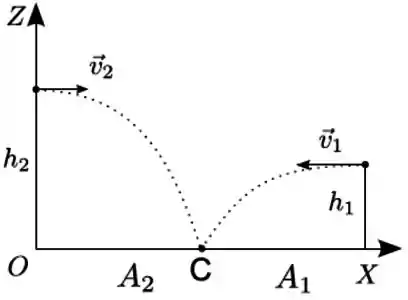
(e) , pois tanto a energia mecânica do bloco como a da esfera se conserva.

Dois projéteis 1 e 2 são lançados simultaneamente e horizontalmente de alturas e (diferentes) em relação ao solo. Verifica-se que ambos atingem o mesmo ponto no solo e têm o mesmo alcance . A razão entre os módulos e das velocidades de lançamento dos respectivos projéteis 1 e 2 é

(a)

(b)

(c)

(d)

(e)

Uma partícula desloca-se ao longo do eixo sob a ação de uma força conservativa , correspondente a uma energia potencial , dada pelo gráfico da figura, na qual o ponto é um ponto de máximo e é um ponto de mínimo. Para esse potencial, entre as opções abaixo a única incorreta é

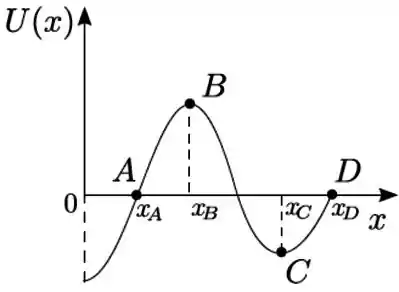
(a) na posição a força sobre a partícula é nula;

(b) na posição , tem-se a condição de equilíbrio estável;

(c) o sentido da força na posição é positivo;

(d) no deslocamento do corpo de para o trabalho realizado pela força é positivo;

(e) na posição a força é nula.

Um bloco encontra-se em repouso sobre um plano inclinado como indicado na figura. Dentre os diagramas e , o que melhor representa (ilustrada por uma seta) a força total que o bloco exerce sobre o plano inclinado é

(a) nenhum dos diagramas;

(b) ;

(c) ;

(d) ;

(e) ;