Energia Potencial e Conservação de Energia
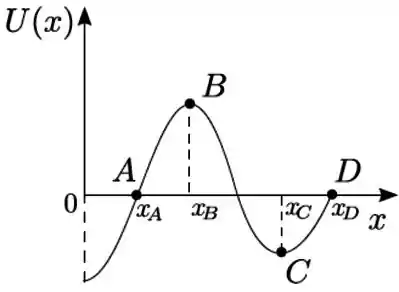
Uma partícula desloca-se ao longo do eixo sob a ação de uma força conservativa , correspondente a uma energia potencial , dada pelo gráfico da figura, na qual o ponto é um ponto de máximo e é um ponto de mínimo. Para esse potencial, entre as opções abaixo a única incorreta é
(a) na posição a força sobre a partícula é nula;
(b) na posição , tem-se a condição de equilíbrio estável;
(c) o sentido da força na posição é positivo;
(d) no deslocamento do corpo de para o trabalho realizado pela força é positivo;
(e) na posição a força é nula.
Passo 1
Vamos ver as alternativas uma por uma!
Alternativa (a): “na posição a força sobre a partícula é nula”
Observamos que:
O ponto é ponto de máximo do gráfico.
Sabemos que:
Nos pontos extremos do gráfico da energia potencial pela posição, a força sobre a partícula é nula.
Portanto:
A alternativa é verdadeira.
Passo 2
Alternativa (b): “na posição , tem-se a condição de equilíbrio estável”
Observamos que:
O ponto é ponto de mínimo do gráfico.
Sabemos que:
Nos pontos de mínimo do gráfico da energia potencial pela posição, ocorre a condição de equilíbrio estável.
Portanto:
A alternativa é verdadeira.
Passo 3
Alternativa (c): “o sentido da força na posição é positivo”
Observamos que:
No ponto A o gráfico é crescente.
Sabemos que:
Quando o gráfico da energia potencial pela posição é crescente, a força é negativa.
Portanto:
A alternativa é falsa.
Passo 4
Alternativa (d): “no deslocamento do corpo de para o trabalho realizado pela força é positivo”
Observamos que:
No deslocamento de pra , a energia potencial diminui.
Sabemos que:
Quando a energia potencial diminui, pra compensar essa perda o trabalho realizado é positivo.
Portanto:
A alternativa é verdadeira.
Passo 5
Alternativa (e): “na posição a força é nula”
Observamos que:
O ponto é ponto de mínimo do gráfico.
E já vimos que:
Nos pontos extremos do gráfico da energia potencial pela posição, a força sobre a partícula é nula.
Portanto:
A alternativa é verdadeira.
Resposta
Alternativa (c)