P2 de Física 1 da UFRJ - 2016.1

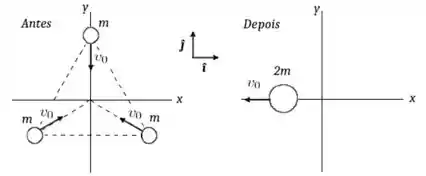
Três átomos idênticos de massa se deslocam no plano horizontal com velocidade de mesmo módulo , de tal forma que os três colidem num determinado ponto. Antes da colisão, os átomos encontram-se sempre equidistantes um do outro conforme mostra a figura. Após a colisão, verifica-se que dois dos átomos formam uma molécula de massa , que se move ao longo do sentido negativo do eixo , com uma velocidade de modulo . O terceiro átomo move-se isoladamente após a colisão. Responda as questões abaixo usando como dados e .

A) Mostre que a velocidade do centro de massa do sistema formado pelos três átomos é nula.

B) Calcule o vetor velocidade do terceiro átomo após a colisão no sistema de coordenadas indicado na figura.

C) Calcule a variação da energia cinética do sistema devido à colisão.

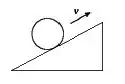
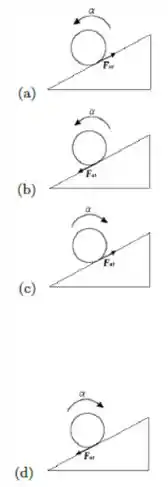
Um tambor cilíndrico rola sem deslizar sobre um plano inclinado. Além da força peso, apenas a superfície exerce força sobre o tambor. Em um determinado instante o tambor sobe o plano inclinado, com velocidade do centro de massa , conforme indicado na figura. Assinale a alternativa que melhor representa o sentido da força de atrito () no ponto de contato entre o plano e o tambor e o sentido da aceleração angula do tambor ()

Duas partículas orbitam em torno uma da outra devido à ação da força gravitacional entre elas. Supondo que não atuam outras forças sobre o sistema assinale das afirmativas apresentadas abaixo, aquelas que são corretas

(I) A órbita de uma partícula em torno da outra será sempre circular

(II) O vetor posição relativo de uma partícula com relação à outra varrerá áreas iguais em intervalos de tempo iguais

(III) A energia cinética associada ao movimento do centro de massa do sistema se conservará

(a) Apenas (II) e (III)

(b) Apenas (I) e (II)

(c) Apenas (I) e (III)

(d) Apenas (II)

(e) Todas estão corretas

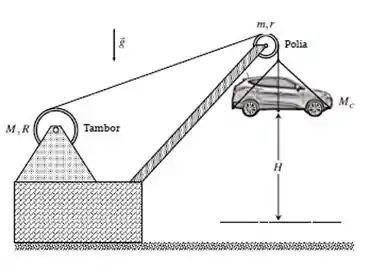
Em uma exposição para vendas, um carro de massa é mantido a uma certa altura do solo através de um cabo ligado a um guindaste. Em um dado instante a trava que mantém o carro elevado falha e ao mesmo tempo começa a cair, fazendo o cabo desenrolar do tambor (cilindro maciço de raio e massa ) e girar a polia superior de raio e massa .

Após cair por uma distância o sistema de segurança da máquina é acionado, fazendo com que o carro pare. Durante a queda, pode-se desprezar deslizamentos no movimento do cabo pelo tambor e pela polia.

Responda as perguntas abaixo desprezando a massa do cabo e apresente as respostas em função de , , , , , e .

(a) Calcule o módulo da velocidade do carro no instante imediatamente anterior ao acionamento do sistema de segurança.

(b) Calcule o módulo da aceleração do carro durante sua queda

(c) Calcule o módulo da tensão no cabo no trecho entre o tambor e a polia durante a queda do carro

ENUNCIADO A: Após um acidente, dois astronautas se encontram isolados no espaço, ligados por um cabo esticado de comprimento , e, girando com velocidade angular em relação a um eixo ortogonal ao cabo e que passa pelo centro de massa do sistema formado por eles (ver figura). Podemos considerar que as dimensões dos astronautas são muito menores que a extensão do cabo e, trata-los como se fossem duas partículas

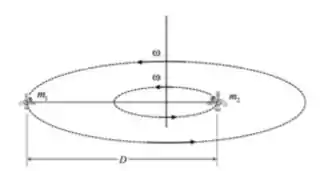
Considere o problema apresentado ENUNCIADO A. Em um dado instante, os dois astronautas começam a se aproximar puxando o cabo. Das afirmações abaixo, assinale aquelas que são corretas.

(I) O momento de inércia de cada astronauta em relação ao eixo de rotação é tal que

(II) O momento angular do sistema em relação ao eixo apresentado se manterá constante

(III) Quando a distância entre os astronautas tiver sido reduzida pela metade a velocidade angular deles será .

1. Todas as afirmações são corretas
2. Apenas (I) e (II)
3. Apenas (I)
4. Apenas (III)
5. Apenas (II) e (III)

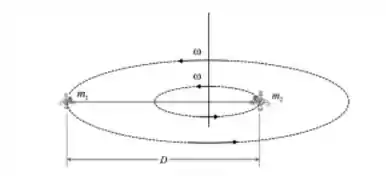
Após um acidente, dois astronautas se encontram isolados no espaço, ligados por um cabo esticado de comprimento , e, girando com velocidade angular em relação a um eixo ortogonal ao cabo e que passa pelo centro de massa do sistema formado por eles (ver figura). Podemos considerar que as dimensões dos astronautas são muito menores que a extensão do cabo e, trata-los como se fossem duas partículas. Sabendo que os dois astronautas têm massas relacionadas por , calcule o raio da trajetória circular do astronauta de massa

a)

b)

c)

d)

e)

O gráfico abaixo mostra o comportamento com o tempo da força que um taco realiza sobre uma bola de golfe de massa , que está inicialmente em repouso quando atingida pelo taco. A força chega a um valor máximo em . Das afirmações que se seguem, assinale aquela que é INCORRETA.

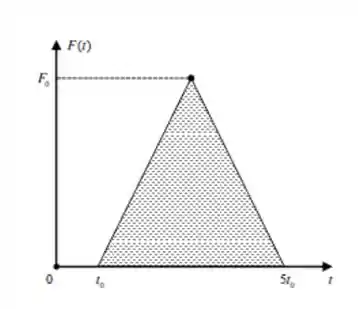
(a) O módulo do impulso produzido pelo taco é dado por

(b) A aceleração média da bola será

(c) A velocidade da bola após a tacada será

(d) A variação de momento linear da bola é fornecida pela área sombreada no gráfico

(e) A aceleração máxima da bola é

Um disco de raio executa um movimento circular, cuja velocidade angular decresce uniformemente. Considere dois pontos e , o ponto sendo localizado na borda do disco, e o ponto sendo localizado a uma distância do centro do disco. Assinale a opção INCORRETA

(a) A aceleração centrípeta do ponto é igual ao triplo da do ponto .

(b) As frequências dos pontos e são iguais.

(c) O módulo da aceleração tangencial do ponto é o triplo da do ponto .

(d) A velocidade linear do ponto é o triplo da do ponto

(e) A velocidade angular instantânea dos pontos e são iguais.

Uma partícula de massa é lançada obliquamente de forma que sua velocidade inicial tem módulo e forma um ângulo com a horizontal. O momento angular da partícula no ponto mais alto de sua trajetória, calculado com relação ao ponto de lançamento tem módulo igual a:

(a)

(b)

(c)

(d)

(e)

(f)

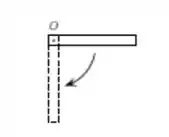
Uma barra uniforme de comprimento e massa está pressa por uma das extremidades a um pivot com atrito desprezível, e, livre para girar no plano vertical. A barra é liberada do repouso na posição horizontal como mostra a figura. Ao atingir a posição vertical, a velocidade linear da extremidade da barra oposta ao pino é

(a)

(b)

(c)

(d)

(e)