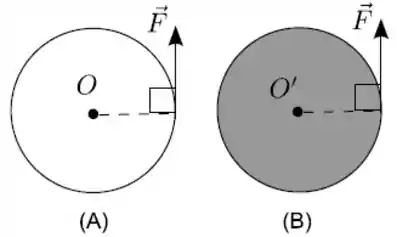
Dois discos e de mesmo raio , constituídos de materiais homogêneos, repousam sobre uma mesa horizontal lisa. Aplica-se a mesma forca a cada disco, tangencialmente às suas respectivas periferias, como indica a figura, fazendo-os girar em torno de um pino central no disco e no disco .
Considerando a massa do disco maior do que a massa do disco , as relações entre os módulos dos torques e , em relação a e , devido À força e os módulos das respectivas acelerações angulares resultantes e são dadas por
(a) e
(b) e
(c) e
(d) e
(e) e
Passo 1
O módulo do torque é dado por
isto é, o módulo da força vezes braço da alavanca.
Nos 2 discos, temos a mesma força (mesmo módulo) atuando a uma mesma distância do eixo de rotação (mesmo braço da alavanca), então o módulo do torque é o mesmo!
Podemos também pensar que a única diferença entre os 2 discos é a massa, e ela não influi no valor do torque :)
Passo 2
A versão pra rotação da 2ª lei de Newton relaciona torque resultante e aceleração angular:
Vamos chamar de e os momentos de inércia dos discos e , respectivamente. As únicas forças realizando torque nos discos são as duas forças , então temos:
Passo 3
Mas acabamos de ver que . Logo,
Os discos têm o mesmo raio , mas como o disco tem maior massa, ele tem maior momento de inércia:
Logo:
Passo 4
Passando pro lado direito da equação:
No entanto, vimos que . Logo, como a aceleração angular é igual à aceleração angular multiplicada por um número menor que :
Resposta
Alternativa (b)