Dois blocos de massas e estão ligados por um fio ideal que passa por uma roldana homogênea, também de massa , e de raio . A roldana é sustentada por um eixo horizontal coincidente com seu eixo geométrico de simetria, como ilustra a figura. Não há atrito entre o eixo e a roldana e o fio não desliza sobre ela. Considere o intervalo de tempo com um instante inicial em que a roldana e os blocos estão em repouso e um instante final em que o bloco mais pesado já desceu uma distância vertical .
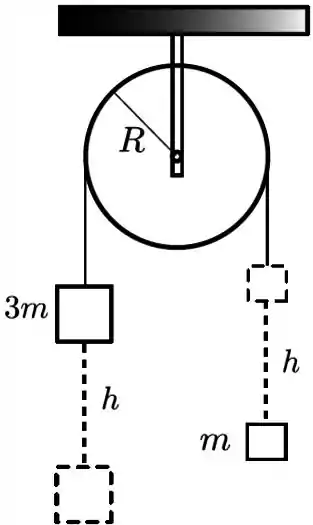
Considere como dados e o módulo da aceleração da gravidade. O momento de inércia da roldana relativo ao seu eixo de simetria é . Calcule
a) a variação da energia cinética do sistema constituído pela roldana e os blocos no intervalo de tempo considerado;
b) o módulo da velocidade do bloco mais pesado no instante final;
c) a razão entre a energia cinética de rotação da roldana e a energia cinética total de translação dos dois blocos no instante final.
Passo 1
a)
Não tem atrito ou outra força não-conservativa atuando no sistema então a energia mecânica do sistema é conservada:
onde é a energia cinética e a energia potencial gravitacional. Então temos
Passo 2
O sistema é composto pela roldana e pelos blocos, mas como a roldana não sai do lugar, sua altura não muda, então sua energia potencial gravitacional é constante. Portanto podemos ignorá-la. Vamos estudar a variação da , então estamos interessados em energias que variam!
Sempre que a gente tem um objeto que não se mexe, podemos fazer isso.
Passo 3
Então vamos focar nas energias potenciais gravitacionais dos blocos, show?
Sendo a variação da energia potencial gravitacional do bloco de massa e a variação de energia potencial gravitacional do bloco de massa , temos
Passo 4
O bloco de massa sobe uma altura , então sua variação de energia potencial gravitacional é:
Passo 5
Já o bloco de massa desce uma altura , então:
Ela é negativa porque o bloco desceu, portanto perdeu energia potencial gravitacional.
Passo 6
Logo, a variação de energia cinética do sistema é:
Passo 7
b)
A primeira coisa que a gente tem que perceber, e que geralmente acontece nos exercícios desse tipo, é que o fio é ideal, então a velocidade dos blocos têm o mesmo módulo!
Queremos achar esse módulo no momento final, então vamos chamá-lo de , beleza?
Passo 8
Agora vamos continuar, tentando aproveitar o resultado da letra (a)!
A energia cinética final do sistema é a soma das energias cinéticas finais da roldana () e dos blocos e ):
Passo 9
Já vimos que os blocos têm velocidade final . Já a roldana não tem translação, sua energia cinética é de rotação, então temos
Passo 10
Mas a roldana está vinculada aos blocos, então podemos usar a relação
Passo 11
E sabemos que o momento de inércia da roldana é
Então a equação vai ficar:
Passo 12
Mas o sistema parte do repouso: a sua energia cinética inicial é nula!
Então a variação de energia cinética do sistema é igual à sua energia cinética final :
Passo 13
É agora que entra o resultado da letra (a)! :D
Vimos que
E depois achamos
Passo 14
Igualando os 2 resultados, isso dá:
Passo 15
c)
Já vimos que a energia cinética de rotação da roldana é:
Substituindo e isso dá:
Passo 16
A energia cinética total final de translação dos blocos é a soma das energias cinéticas finais dos 2 blocos:
Passo 17
Então a razão entre a energia cinética de rotação da roldana e a energia cinética de translação dos blocos é:
Resposta
a)
b)
c)