P2 de Física 1 da USP - 2010

Uma pessoa de 60 kg, correndo inicialmente com uma velocidade de 4 m/s pula em um carrinho de 120 kg que encontra-se inicialmente em repouso. Ao pular, a pessoa escorrega, vindo a deslizar sobre a superfície superior do carrinho até parar, ficando em repouso em relação a este. O coeficiente de atrito cinético entre a pessoa e a superfície do carrinho é de 0,4. O atrito entre o carrinho e o solo pode ser desprezado. Pede-se calcular:

1. A velocidade final do sistema carrinho mais pessoa em relação ao solo.
2. A força de atrito atuando sobre a pessoa enquanto ela está deslizando.
3. O trabalho realizado pela força de atrito e o deslocamento da pessoa sobre a superfície do carrinho em relação ao carrinho.
4. A variação da energia cinética do carrinho.

Um trem é carregado com areia ao passar sob uma ponte. A areia é despejada nos vagões à taxa de 500kg por segundo. Como a areia é despejada verticalmente de uma altura de vários metros, ao atingir a caçamba do vagão, a velocidade dos grãos de areia é de cerca de 14m/s. A massa do vagão vazio é de 2.000kg, e é preenchido

com 6.000kg de areia ao passar sob a ponte.

1. Desprezando-se as perdas por atrito com os trilhos, determine a força que a locomotiva precisa fazer para puxar o trem a uma velocidade constante de 0,5m/s e a potência necessária para manter o movimento. Note que como o sistema não pode ser considerado como uma partícula não é conveniente a utilização do teorema trabalho-energia cinética.
2. Determine a força suportada pelo trecho de trilhos sob um vagão quando este estiver 50% preenchido de areia. Suponha que o trecho de trilhos em questão suporta somente este vagão neste momento.
3. Se a locomotiva desengatar do primeiro vagão quantos segundos se passarão até que o restante do trem reduza sua velocidade à metade da inicial? Suponha que a massa do restante do trem (incluindo a areia) seja de 10.000kg no instante do desengate.

Considere um potencial, descrevendo uma força conservativa, dado pela função:

1. Faça o gráfico da função potencial e da força associada a este potencial, indicando os pontos de máximo e mínimos locais, os pontos que e , e os valores assintóticos para os limites de e
2. Desejamos empregar este potencial para aprisionar uma partícula de massa M. Qual é a velocidade máxima da partícula, em x = 0, para que a mesma fique confinada no potencial?
3. Para uma partícula com velocidade , vinda de A, podemos realizar o aprisionamento adicionando uma força dissipativa: na região entre , a partícula sofre pequenas variações de momento , opostas ao seu deslocamento, a um intervalo médio (muito menor que o tempo de voo nesta região), resultando em uma força de atrito constante se sua velocidade não for nula. Qual a velocidade máxima de aprisionamento da partícula em função dos parâmetros desta armadilha?

Num parque de diversões, um carrinho desce sem atrito de uma altura para dar a volta num loop circular de raio , conforme mostrado na figura.

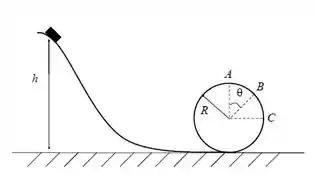
1. Qual é o menor valor de (chame este valor ) necessário para que o carrinho faça a volta completa do loop?
2. Se , o carrinho cai do trilho em um ponto B, quando ainda falta percorrer mais um ângulo para chegar até o topo A. Calcule .
3. Suponha que agora, por alguma razão, haja atrito cinético entre o carrinho e o trilho. Sabendo que o carrinho foi solto (no repouso) da altura e que ele passou no ponto C do loop com velocidade escalar , qual é o trabalho realizado pela força de atrito até o ponto C?