Trabalho e Energia Cinética, Energia Potencial e Conservação de Energia, Forças e Leis de Newton, Força Centrípeta
Num parque de diversões, um carrinho desce sem atrito de uma altura para dar a volta num loop circular de raio , conforme mostrado na figura.
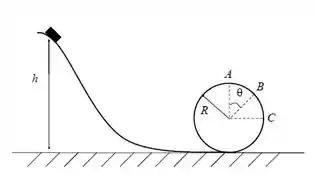
- Qual é o menor valor de (chame este valor ) necessário para que o carrinho faça a volta completa do loop?
- Se , o carrinho cai do trilho em um ponto B, quando ainda falta percorrer mais um ângulo para chegar até o topo A. Calcule .
- Suponha que agora, por alguma razão, haja atrito cinético entre o carrinho e o trilho. Sabendo que o carrinho foi solto (no repouso) da altura e que ele passou no ponto C do loop com velocidade escalar , qual é o trabalho realizado pela força de atrito até o ponto C?
Passo 1
Essa é uma questão que envolve principalmente conservação da energia mecânica e Leis de Newton. Os dados que nos deram foram:
Passo 2
- A menor altura é aquela que a normal no ponto mais alto da trajetória, nesse caso no ponto A, é zero.
Ué, mas por quê?
Normal nada mais é que uma força de contato entre dois corpos, quando um objeto está na iminência de perder o contato a normal é nula, sacou?
Daí, fazendo o diagrama de forças, podemos observar que:
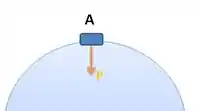
Como o nosso carrinho está em um movimento de rotação em torno de um ponto,fazendo uma órbita circular de raio R, podemos dizer que, naquele ponto, a componente centrípeta é apenas o peso, pois:
Como no ponto A, os vetores gravidade e aceleração centrípeta apontam para baixo, podemos cortar os vetores unitários e utilizar apenas os escalares, na forma:
Mas, mano! Pra que isso se nessa relação nem apareceu o
Passo 3
Sabemos ainda que a aceleração centrípeta pode ser calculada por:
E daí concluímos nossa primeira equação:
Passo 4
Mas, mano! Pra que isso se nessa relação nem apareceu o
Saca só! Podemos também utilizar a conservação da energia mecânica que vai aparecer um termo com “” e com “”. Daí a gente corta tudo! Bora ver?
Sendo e , teremos:
Cortando os “” e ajeitando as contas, teremos:
Passo 5
Mas a gente viu que lá no Passo 3, daí, substituindo, teremos:
Passo 6
b)
Este caso teremos a mesma causa da questão a, porém em uma situação diferente. Com teremos que ele não vai chegar no ponto A, logo a normal será zero antes do ponto A. Vamos ver o diagrama de forças na figura abaixo:
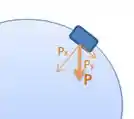
Podemos notar que, como não há normal, somente haverá a força peso como força resultante. Decompondo-a em resultante centrípeta e tangencial e aplicando as Leis de Newton, teremos:
Como a parte tangencial pouco interessa para a gente, vamos trabalhar com a parte centrípeta!
Passo 7
Agora, como na letra a, vamos utilizar a conservação da energia cinética para achar uma relação entre e .
Pela conservação da Energia Cinética, teremos:
Passo 8
Sendo o a altura em que o carrinho se desligará do percurso. Para achar em função das demais variáveis, podemos notar que:
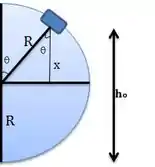
Ah, mas da relação da figura acima, podemos ver que , logo:
Jogando na equação do passo anterior, a gente vai ter:
Passo 9
Da equação que encontramos no Passo 6, a gente vai ter:
Por fim, isolando o ...
Passo 10
c)
Pois bem! Aqui ele nos diz que o carrinho desce de uma altura , passa por um atrito maroto até chegar no ponto C, com altura R e velocidade .
Vamos pensar da seguinte forma:
Inicialmente só temos a energia potencial que ao ser solto gerará movimento, certo?
Em seguida, ele vai ser freado pelo atrito e pela subida até a altura R chegando em c com velocidade
Dá pra enxergar uma relação do “antes-depois”, que será dada por: