P3 de Física 1 da USP - 2013

Um cilindro maciço de massa e raio é acelerado por uma força de tração , conforme mostrada na figura, aplicada através de uma corda enrolada em torno de um tambor de raio conectado concentricamente ao centro do cilindro. Despreze a massa da corda e do tambor e assuma o movimento na horizontal. O coeficiente de atrito estático é suficiente para que o cilindro role sem deslizar. Considerando que a aceleração do cilindro é e que o momento de inércia é :

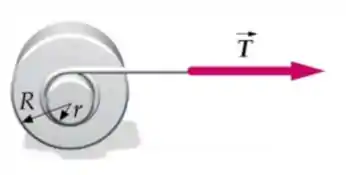
Determine a força de atrito em função de ,,,.

Qual valor de para que a aceleração do cilindro seja maior que .

Uma barra delgada homogênea de comprimento e massa está inicialmente em repouso como mostra a figura. Preso a uma de suas extremidades há um objeto de massa e dimensões desprezíveis. Um segundo objeto do mesmo tipo move-se na direção do eixo , com velocidade constante. No instante o segundo objeto atinge a outra ponta da barra e adere a ela de forma permanente. Não há atrito no movimento dos objetos sobre o plano horizontal . Use para descrever o movimento da barra o ângulo entre a barra e o eixo , considerando como positivo o sentido anti-horário.

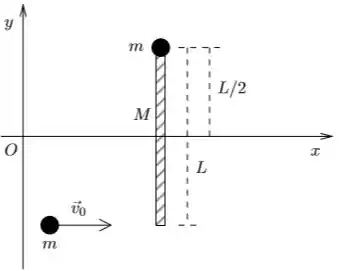
Determine o momento de inércia do conjunto de corpos, depois do choque, em relação a um eixo na direção , passando pelo centro de massa.

Determine a velocidade do centro de massa do conjunto de corpos, depois do choque.

Determine a velocidade angular do conjunto de corpos, depois do choque, em relação a um eixo na direção , passando pelo centro de massa.

Determine a velocidade do segundo corpo, depois do choque, em relação à origem do sistema de coordenadas mostrado na figura.

Um cilindro oco (raio , ) rola para baixo em um plano inclinado (ângulo ) sem deslizar. Sobre a superfície do cilindro corre um menino (massa , que pode ser considerada como puntiforme), e ele consegue ficar sempre no ponto mais alto do cilindro. Considere .

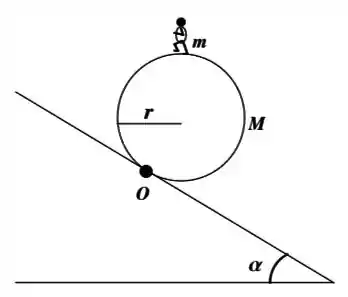
Calcule o momento de inércia do cilindro em relação ao eixo instantâneo .

Ache a expressão para momento angular do sistema em torno do ponto em termos das massas, ângulo, raio e velocidade do centro de massa.

Qual é o torque total de forcas externas sobre o sistema em relação do ponto ?

Calcule o módulo da aceleração do cento de massa do cilindro.