Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Momento Angular

Ver Teoria
Exercício 201234567891011121314151617181921222324252627282930313233343536373839404142434445464748495051525354555657585960616263646566676869707172737475767778798081828384858687888990919293949596979899100

Enunciado

Rotação, Dinâmica de Rotação, Momento Angular, Corpos Rígidos

Um cilindro oco (raio r = 0.5   m , M = 15   k g ) rola para baixo em um plano inclinado (ângulo α = π 6 ) sem deslizar. Sobre a superfície do cilindro corre um menino (massa m = 30   k g , que pode ser considerada como puntiforme), e ele consegue ficar sempre no ponto mais alto do cilindro. Considere g = 10 m / s 2 .

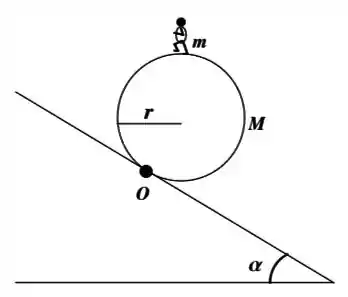
a ) Calcule o momento de inércia do cilindro em relação ao eixo instantâneo O .

b ) Ache a expressão para momento angular do sistema em torno do ponto O em termos das massas, ângulo, raio e velocidade do centro de massa.

c ) Qual é o torque total de forcas externas sobre o sistema em relação do ponto O ?

d ) Calcule o módulo da aceleração do cento de massa do cilindro.

Passo 1

a )

Usando o teorema dos eixos paralelos:

I O = I C M + M r 2

I O = M r 2 + M r 2

I O = 2 M r 2

I 0 = 2   .   15   .   0,5 2

I O = 7,5   k g . m 2

Passo 2

b )

Neste caso o momento angular será dado por:

L O = L c i l i n d r o + L m e n i n o

Onde:

L c i l i n d r o = I O ω

E lembrando-se da definição L → = r → × m v → :

L m e n i n o = m . v . l

Onde l é distancia perpendicular do ponto O à linha da direção do vetor v → . E a velocidade v do menino é igual à velocidade do centro de massa.

Logo:

L O = I O ω + m v l

Da geometria:

l = r ( 1 + cos ⁡ α )

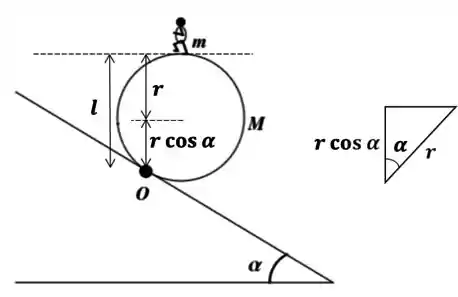
Como o cilindro rola sem deslizar podemos utilizar a relação:

v = ω . r

ω = v r

Substituindo em no momento angular temos

L O = I O ω + m . v . l

L O = 2 M r 2 . v r + m . v . r ( 1 + cos ⁡ α )

L O = 2 M + m 1 + cos ⁡ α r . v

Passo 3

c )

Torque da força do peso:

τ O = r → × F →

Pegando apenas a parte perpendicular da distância

τ O = r sen ⁡ α . M + m g

τ O = M + m g . r sen ⁡ α

Passo 4

d )

O Centro de massa e o eixo de rotação O se movem paralelo.

Da fórmula temos:

d L O d t = τ O

E também temos:

d L O d t = d d t 2 M + m 1 + cos ⁡ α r . v

d L O d t = ( 2 M + m ( 1 + cos ⁡ α ) r a

Igualando as fórmulas temos:

τ O = ( 2 M + m ( 1 + cos ⁡ α ) r a

M + m g . r sen ⁡ α = ( 2 M + m ( 1 + cos ⁡ α ) r a

a = ( M + m ) g sen ⁡ α 2 M + m 1 + cos ⁡ α

a = 15 + 30 10   . 1 2 2   .   15 + 30 1 + 3 2

a = 2   .   45   .   5 2   .   30 + 30 2 + 3

a = 90   .   5 30 4 + 3

a ≅ 15 5,73

a ≅ 2,6   m / s 2

Resposta

a )   I O = 7,5   k g . m 2

b )   L O = 2 M + m 1 + cos ⁡ α r . v

c )   τ O = M + m g . r sen ⁡ α

d )   a ≅ 2,6   m / s 2

Exercícios de Livros Relacionados

Um bloco homogênea de granito em forma de livro possui faces de 20c m por 15c m e uma espessura de 1,2c m . A massa específica (massa por unidade de volume) do granito é 2,64g / c m 3 . O bloco gira e
10.19E Calcule o momento angular orbital da Terra em termos da constante de Planck.
Um ponto na borda de um rebolo com 0,75m de diâmetro muda de velocidade, a uma taxa constante, de 12m / s para 25m / s em 6,2s . Qual é a aceleração angular média do rebolo?
Em um certo instante, uma partícula de 0,80k g está situada na posição r → = 2,0m i ^ + 3,0m j ^ . O momento linear da partícula está no plano x y e tem um módulo de 2,4k g ∙ m / s e uma direção de 11
Em um certo instante, a força F → = 4 j → N age sobre um objeto de 0,25 k g cujo vetor posição é r → = 2 i → - 2 k → e cujo vetor velocidade é v → = - 5 i → + 5 k → . Em relação à origem e em termos d