Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Conservação do Momento Angular

Ver Teoria
Exercício 181234567891011121314151617192021222324252627282930313233343536373839404142434445464748495051525354555657585960616263646566676869707172737475767778798081828384858687888990919293949596979899100

Enunciado

Corpos Rígidos, Momento Linear, Momento Angular, Dinâmica de Rotação

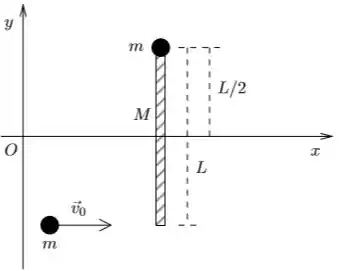
Uma barra delgada homogênea de comprimento L e massa M está inicialmente em repouso como mostra a figura. Preso a uma de suas extremidades há um objeto de massa m e dimensões desprezíveis. Um segundo objeto do mesmo tipo move-se na direção do eixo x , com velocidade v 0 → constante. No instante t = 0 o segundo objeto atinge a outra ponta da barra e adere a ela de forma permanente. Não há atrito no movimento dos objetos sobre o plano horizontal ( x , y ) . Use para descrever o movimento da barra o ângulo θ entre a barra e o eixo y , considerando como positivo o sentido anti-horário.

a ) Determine o momento de inércia I C M do conjunto de corpos, depois do choque, em relação a um eixo na direção z ^ , passando pelo centro de massa.

b ) Determine a velocidade V → do centro de massa do conjunto de corpos, depois do choque.

c ) Determine a velocidade angular ω → do conjunto de corpos, depois do choque, em relação a um eixo na direção z ^ , passando pelo centro de massa.

d ) Determine a velocidade v → ( t ) do segundo corpo, depois do choque, em relação à origem O do sistema de coordenadas mostrado na figura.

Passo 1

a )

Dada a simetria do sistema, o centro de massa do conjunto de corpos está sobre o eixo x . O momento de inércia de cada corpo pontual em relação ao centro de massa é dado por:

I = m . r →

I 1,2 = m . L 2 2

I 1,2 = m . L 2 4

O momento de inércia da barra em relação ao centro de massa pode ser calculado como:

I = ∫ r 2   d m

Utilizando a densidade ρ da barra:

ρ = d m d x

d m = ρ   d x

Ficamos com:

I B = ∫ - L 2 L 2 x 2   d m

I B = ∫ - L 2 L 2 x 2 ρ   d x

Lembrando que ρ = M L .

I B = ∫ - L 2 L 2 x 2 . M L   d x

I B = M L ∫ - L 2 L 2 x 2   d x

Resolvendo a integral definida:      

I B = M L x 3 3 - L 2 L 2

I B = M L . 2 L 3 24

I B = M . L 2 12

Segue que o momento de inércia total em relação ao centro de massa é dado pela soma do momento de inercia dos objetos pontuais com o momento de inercia da barra.

I C M = 2 I 1,2 + I B

I C M = 2 m . L 2 4 + M L 2 12

I C M = m 2 + M 12 L 2

I C M = 6 m + M 12 L 2

Passo 2

b )

Como não há forças externas, o momento linear do conjunto de corpos é conservado. O momento linear inicial é dado por:

p i → = m v 0 →

p i → = m v 0 x ^

Onde v 0 → é a velocidade do objeto que se aproxima da barra.

O momento linear final do conjunto de corpos é dado por:

p f → = 2 m + M V →

p f → = 2 m + M V x ^

Como p f → = p i → (conservação do momento linear) temos que:

2 m + M V x ^ = m v 0 x ^

V = m v 0 2 m + M

V → = m v 0 2 m + M x ^

Passo 3

c )

Como não há torques externos, o momento angular do conjunto de corpos em relação à origem O é conservado. O momento angular inicial é dado por:

L → = r → × p →

L → = r → × m v

Como a distancia do objeto ao centro de massa é L 2 , temos que:

L i → = m v 0 . L 2 z ^

O momento angular também pode ser calculado utilizando a relação:

L → = I ω →

Vamos utilizar essa relação para o momento angular final do conjunto de corpos.

L f → = I C M ω →

L f → = 6 m + M 12 L 2 ω z ^

Como L f → = L i → (conservação do momento angular, não há torque externo ao sistema) temos que:

6 m + M 12 L 2 ω z ^ = m v 0 . L 2 z ^

ω = m v 0 . L 2 . 1 L 2 . 12 6 m + M

ω = 6 m 6 m + M . v 0 L

ω → = 6 m 6 m + M . v 0 L z ^

Passo 4

d )

A velocidade v → de um ponto no corpo rígido é dada pela soma de dois movimentos, o de translação e o de rotação.

A translação desse ponto nada mais é do que o deslocamento do centro de massa. Ou seja, a velocidade de translação é a velocidade do centro de massa.

v t r a n s l a ç ã o → = V →

Agora, a rotação desse ponto é dada pela velocidade linear de rotação neste ponto, que conseguimos encontrar com a relação:

v r o t a ç ã o → = ω → × r →

Logo, a velocidade em um ponto do corpo rígido pode ser dada por:

v → = v t r a n s → + v r o t →

v → = V → + ω → × r →

Em nosso caso aqui já temos os valores de V → e ω → , enquanto r → é a posição do segundo corpo pontual em relação ao centro de massa, que é dada por:

r → = L 2 sen ⁡ θ x ^ - cos ⁡ θ y ^

Onde θ = ω t e θ é o ângulo que a barra faz com o eixo y . Segue que temos para a velocidade do segundo corpo pontual:

v → t = m v 0 2 m + M x ^ + 6 m 6 m + M . v 0 L . L 2 z ^ × sen ⁡ ω t x ^ - cos ⁡ ω t y ^

v → ( t ) = m v 0 2 m + M x ^ + 3 m v 0 6 m + M sen ⁡ ω t z ^ × x ^ - cos ⁡ ω t z ^ × y ^

v → ( t ) = m v 0 2 m + M x ^ + 3 m v 0 6 m + M [ cos ⁡ ω t x ^ + sen ⁡ ω t y ^ ]

Resposta

a )   I C M = 6 m + M 12 L 2

b )   V → = m v 0 2 m + M x ^

c )   ω → = 6 m 6 m + M . v 0 L z ^

d )   v → ( t ) = m v 0 2 m + M x ^ + 3 m v 0 6 m + M [ cos ⁡ ω t x ^ + sen ⁡ ω t y ^ ]

Exercícios de Livros Relacionados

Um homem está em pé em uma plataforma que gira (sem atrito) com uma velocidade angular de 1,2 r e v / s ; seus braços estão abertos e ele segura um tijolo em cada mão. O momento de inércia do sistema
Na figura abaixo duas partinadoras com 50kg de massa, que se movem com uma velocidade escalar de 1,4m/s , se aproximam em trajetórias paralelas separadas por 3m . Uma das patinadoras carrega uma vara
Um patinador girando. Podemos considerar as mãos e os braços esticados para fora de um patinador que se prepara para girar como uma barra delgada cujo eixo de giro passa pelo seu centro de gravidade (
Uma barra uniforme de 0,0300 kg e comprimento de 0,400 m gira em um plano horizontal em torno de um eixo fixo passando em seu centro e perpendicular à barra. Dois pequenos anéis, cada um com massa de
Um pequeno inseto de 10,0 g está pousado sobre uma das extremidades de uma barra delgada e uniforme, que está inicialmente em repouso sobre uma mesa horizontal lisa. A outra extremidade da barra pivot