Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Rolamento sem Deslizamento

Ver Teoria
Exercício 171234567891011121314151618192021222324252627282930313233343536373839404142434445464748495051525354555657585960616263646566676869707172737475767778798081828384858687888990919293949596979899100

Enunciado

Corpos Rígidos, Rotação, Dinâmica de Rotação

Um cilindro maciço de massa M e raio R é acelerado por uma força de tração T , conforme mostrada na figura, aplicada através de uma corda enrolada em torno de um tambor de raio r conectado concentricamente ao centro do cilindro. Despreze a massa da corda e do tambor e assuma o movimento na horizontal. O coeficiente de atrito estático é suficiente para que o cilindro role sem deslizar. Considerando que a aceleração do cilindro é a e que o momento de inércia é I = M R 2 2 :

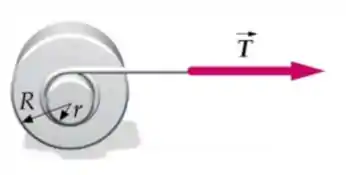
a ) Determine a força de atrito em função de M , a , r , R .

b ) Qual valor de r para que a aceleração do cilindro seja maior que T M .

Passo 1

a )

Vamos primeiramente analisar o movimento de translação do cilindro utilizando a segunda lei de Newton.

F → = m a →

T - F a t = M . a

T = F a t + M . a

Agora vamos aplicar a lei de rotação:

τ → = I α →

Lembrando que τ → = r → × F → :

F a t . R + T . r = I α

Substituindo o T pelo valor que encontramos ao aplicar a lei de translação e o valor do momento de inércia dado pelo enunciado, temos:

F a t . R + F a t + M . a . r = M R 2 2 . α

E agora utilizando a informação de que o cilindro rola sem deslizar, podemos utilizar a relação:

a = α . R

α = a R

Substituindo

F a t . R + F a t + M . a . r = M R 2 2 . a R

Dividindo ambos os lados da equação por R :

F a t + F a t + M . a . r R = M 2 . a

F a t + F a t . r R + M . a . r R = M 2 . a

F a t 1 + r R = M 2 . a - M . a . r R

F a t 1 + r R = M . a 1 2 - r R

F a t R + r R = M . a R - 2 r 2 R

F a t = M . a R - 2 r 2 R R R + r

E finalmente encontramos:

F a t = M . a 2 . R - 2 r R + r

Passo 2

b )

Utilizando a equação de T que encontramos analisando o movimento de translação:

T = F a t + M . a

Substituímos a F a t encontrada no item anterior.

T = M . a 2 . R - 2 r R + r + M . a

Colocando " M . a " em evidência

T = M . a R 2 - r R + r + 1

T = M . a R 2 - r + R + r R + r

T = M . a . 3 2 R R + r

a = T M . 2 3 R + r R

Logo, para que a > T M , temos que ter obrigatoriamente.

2 3 R + r R > 1

2 R + 2 r > 3 R

r > R 2

Resposta

a )   F a t = M . a 2 . R - 2 r R + r

b )   r > R 2

Exercícios de Livros Relacionados

Um mecanismo em forma de ioiô, montado em um eixo horizontal sem atrito, é usado para levantar uma caixa de 30kg , como mostra a figura abaixo. O raio externo R da roda é 0,5m e o raio r do cubo da ro
Na Fig. 11-60, uma força horizontal constante F → de módulo 12N é aplicada a um cilindro maciço homogêneo através de uma linha de pescar enrolada no cilindro. A massa do cilindro é 10k g , o raio é 0,
10.3E Um cilindro rola em uma rampa de inclinação θ = 30 ° . A) Calcule a aceleração angular do cilindro B) Calcule a força de atrito da rampa sobre o cilindro.
10.7P Calcule em termos do raio R da bola, o parâmetro de impacto b de uma tacada com que um jogador deve chutar uma bola para que esta tenha uma velocidade angular vertical dada por ω = v / 2 R .
Um ioiô possui um momento de inércia de 950 g c m ² ² e uma massa de 120 g . O raio do eixo é 3,2 m m e a corda tem 120 c m de comprimento. O ioiô rola para baixo, a partir do repouso, até a extremida