3º EE de Física 2 da UFPE - 2015.2

Uma onda harmônica se propaga em uma corda fazendo a corda oscilar na direção . A massa específica linear da corda é . Os deslocamentos da corda nas posições e variam com o tempo de acordo com as seguintes equações:

Onde o tempo está em segundos, ao passo que estão em centímetros.

1. Quais são a amplitude e o período dessa onda harmônica?
2. Se for o valor do comprimento de onda em metros, qual será a tensão na corda em termos de ?
3. Qual é o maior comprimento de onda compatível com os dados do enunciado?

Dica: Note que a função pode ser equivalentemente escrita como para qualquer número inteiro , ou seja, uma fase de pode ter sido omitida no enunciado. Por isso, há vários valores possíveis para o número de onda angular.

Observa-se que o ângulo entre um pêndulo simples e sua posição de equilíbrio varia da seguinte forma no tempo:

Onde o tempo está em segundos e o ângulo em radianos. Qual das afirrmações abaixo descreve melhor o sistema:

a) O pêndulo oscila livremente, sem atrito e sem força externa periódica;

b) O pêndulo está sofrendo uma força externa de frequência não sofre atrito;

c) O pêndulo está sofrendo uma força externa de frequência e não sofre atrito;

d) O pêndulo está sendo empurrado periodicamente com frequência igual à frequência de ressonância.

e) O pêndulo está sofrendo uma força de atrito e não sofre uma força externa periódica.

Um bloco preso a uma mola executa um movimento harmônico simples. No instante, o bloco está exatamente no ponto intermediário entre a posição de equilíbrio da mola e a posição na qual a distensão da mola é máxima.Pode-se dizer que, nesse instante , a energia cinética do sistema massa-mola é:

1. 3 vezes maior que a energia potencial elástica.
2. 2 vezes maior que a energia potencial elástica.
3. igual à energia potencial elástica.
4. da energia potencial elástica.
5. da energia potencial elástica.
6. Impossível de ser comparada à energia potencial elástica.

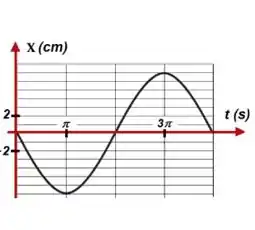
A figura ao lado mostra o deslocamento de um bloco preso a uma mola executando uma movimento harmônico simples. Qual é o módulo da velocidade máxima que o bloco pode ter? A resposta deve estar na unidade

Três alto-falantes , e emitem ondas sonoras idênticas e em fase. Os alto-falantes estão em posições diferentes em relação ao detector , mas todos estão contidos em um mesmo plano, como ilustrado na figura ao lado.

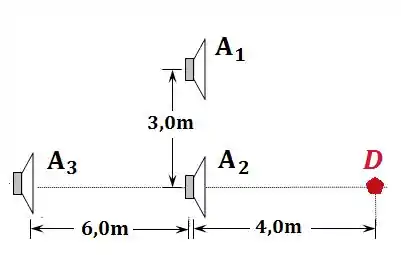
1. Suponha que o alto-falante está desligado, ou seja, considere apenas os alto-falantes e . Nesse caso, quais são os comprimentos de onda que fazem com que nenhum sinal sonoro chegue ao detector ?
2. Agora, suponha que o alto-falante foi ligado, de forma que os três alto-falantes estão emitindo ondas sonoras. Nesse caso, qual é a menor frequência que faz com que o som que chegue ao detector tenha a maior amplitude possível?

Dados:

Marque a alternativa Errada:

a) Quando fazemos a corda de um violão soar, formam-se ondas estacionárias e escutamos as frequências de ressonância da corda.

b) Se quadruplicarmos a tensão de uma corda cujas extremidades estão fixas, a frequência de ressonância fundamental dobrará..

c) Enquanto uma onda progressiva se propaga em uma corda esticada, a quantidade de energia em cada pedaço da corda não é constante, pois a energia é transportada pela onda.

d) A velocidade de propagação de uma onda harmônica em uma corda cresce linearmente quando aumentamos a frequência da onda.

e) As velocidades máximas das partículas de uma corda oscilante dependem da amplitude e da frequência da oscilação.

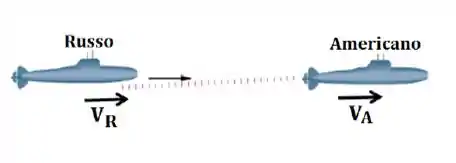
Um submarino Russo com velocidade está seguindo um submarino Americano que move-se com velocidade , conforme ilustrado ao lado. O submarino Russo emite uma onda sonora com frequância e que se propaga na água do mar com velocidade . Qual frequância é detectada pelo submarino americano?