Exercícios Resolvidos de Interferência de Ondas Sonoras

Ver Teoria

Exercício 15 1 2 3 4 5 6 7 8 9 10 11 12 13 14 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36

Enunciado

Origem do Exercício

Três alto-falantes , e emitem ondas sonoras idênticas e em fase. Os alto-falantes estão em posições diferentes em relação ao detector , mas todos estão contidos em um mesmo plano, como ilustrado na figura ao lado.

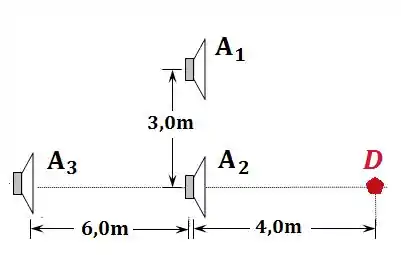
Suponha que o alto-falante está desligado, ou seja, considere apenas os alto-falantes e . Nesse caso, quais são os comprimentos de onda que fazem com que nenhum sinal sonoro chegue ao detector ?

Agora, suponha que o alto-falante foi ligado, de forma que os três alto-falantes estão emitindo ondas sonoras. Nesse caso, qual é a menor frequência que faz com que o som que chegue ao detector tenha a maior amplitude possível?

Dados:

Passo 1

Primeiro vamos calcular as distâncias dos transmissores ao detector:

A distância do transmissor ao detector é , e é dada por:

E a distância entre e o detector é:

Para que nenhum sinal chegue ao detector, é preciso que haja uma interferência destrutiva.

Assim:

Passo 2

Para que o som tenha a maior amplitude possível, é preciso que as três fontes gerem apenas interferências construtivas. Assim, lembrando que para uma interfeência construtiva:

Vamos, então, analisar as interferências que podem acontecer.

Interferência construtiva entre

Devemos considerar apenas o caso em que as três interferências são construtivas, ou seja, quando:

Isso nos leva à:

Assim, o maior comprimento vai ser , quando

Usando o valor da velocidade do som, podemos achar a frequência:

Resposta

Exercícios de Livros Relacionados

A figura mostra duas fontes pontuais F 1 e F 2 que emitem sons de comprimento de onda λ = 2,00m . As emissões são isotrópicas e em fase; a distância entre as fontes é d = 16,0m . Em qualquer ponto P s

Uma onda sonora senoidal se propaga no ar, no sentido positivo de um eixo x , com uma velocidade de 343 m / s . Em um certo instante, a molécula A do ar está em seu deslocamento máximo no sentido nega

Na figura abaixo temos as ondas sonoras A e B , de mesmo comprimento de onda λ , estão inicialmente em fase e se propagam para a direita, como indicam os dois raios. A onda A é refletida por quatro su

Duas ondas sonoras, produzidas por duas fontes diferentes de mesma frequência, 540H z , se propagam na mesma direção e no mesmo sentido a 330m / s . As fontes estão em fase. Qual é a diferença de fase

Na figura, um som com um comprimento de onda de 40,0c m se propaga para a direita através de um tubo que possui uma bifurcação. Ao chegar à bifurcação, a onda se divide em duas partes. Uma parte se pr