Origem do Exercício
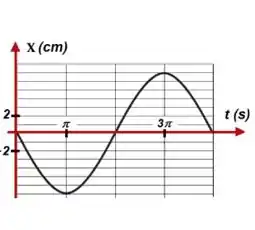
A figura ao lado mostra o deslocamento de um bloco preso a uma mola executando uma movimento harmônico simples. Qual é o módulo da velocidade máxima que o bloco pode ter? A resposta deve estar na unidade
Passo 1
Bom, o enunciado diz que o movimento é um MHS. Assim, a posição é dada por:
Beleza? E como será a velocidade? Será a derivada dessa função:
Passo 2
Beleza, e qual vai ser a velocidade máxima? A velocidade será máxima, em módulo, acontecerá quando a função seno tiver seu valor máximo, assim:
Passo 3
Agora é só a gente analisar ao gráfico: Por ele, notamos que:
Assim:
Assim:
Assim:
m)
Resposta
m)
Exercícios de Livros Relacionados
A função x = 6,0m c o s [ ( 3 πr a d / s )t+ π / 3r a d ] descreve o movimento harmônico simples de um corpo. No instante t = 2,0s , qual é (a) o deslocamento, (b) a velocidade, (c) a aceleração e (
Duas partículas oscilam em movimento harmônico simples ao longo de um segmento retilíneo comum de comprimento A . As duas partículas têm um período de 1,5s , mas existe uma diferença de fase π / 6r a
Um objeto que executa um movimento harmônico simples leva 0,25s para se deslocar de um ponto de velocidade nula para o ponto seguinte do mesmo tipo. A distância entre esses pontos é 36c m . Calcule (a
Uma partícula executa um MHS linear com uma frequência de 0,25 H z em torno do ponto x = 0 . Em t = 0 , a partícula tem um deslocamento x = 0,37 c m e velocidade nula. Determine os seguintes parâmetro
13.10. Arrancada. A corda de um violão vibra com uma frequência igual a 440 Hz. Um ponto em seu centro se move com MHS com amplitude igual a 3,0 mm e um ângulo de fase igual a zero. a) Escreva uma equ