P1 de Física 3 - FIS1051 da PUCRIO - 2017.1

Três cargas puntiformes de igual valor e idênticas massas , são penduradas de um ponto comum por fios isolantes, todos de comprimento . Na situação de equilíbrio, o arranjo fica como ilustrado na Figura ao lado (considere a aceleração da gravidade conhecida).

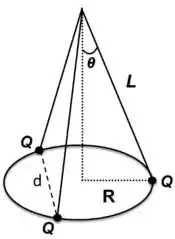
a) Calcule a distância, , de equilíbrio entre as cargas em função de (veja o desenho).

b) Calcule o valor da força elétrica resultante sobre cada uma das cargas devido à ação das demais. Expresse seu resultado em termos do ângulo e do comprimento .

c) Calcule o valor de cada carga em função de , e (Sugestão: lembre-se que no equilíbrio a força total resultante nas cargas deve ser igual a zero).

Considere o bastão delgado da figura, de comprimento , posicionado ao longo do eixo . Sobre o bastão existe uma densidade linear de carga dada por , onde é uma constante positiva (todas as unidades estão no SI). Um determinado ponto possui coordenadas retangulares onde .

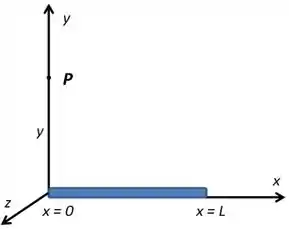
a) Considerando a referência dos potenciais no infinito encontre o potencial no ponto .

b) Suponha agora que o potencial gerado pelo bastão no ponto seja dado pela expressão:

onde é uma constante positiva (todas as unidades estão no SI). Calcule a componente do vetor campo elétrico em a partir da expressão fornecida. Responda também se as componentes e do vetor campo elétrico em , devidas ao bastão com a densidade linear de carga original, são positivas, negativas ou nulas, sem precisar calculá-las diretamente a partir da lei de Coulomb (Sugestão: use argumentos de simetria).

Considere novamente a expressão dada no item (b), agora com os valores numéricos , e em unidades do SI.

c) Calcule todos os pontos do espaço em que a carga puntiforme pode ser colocada de modo que o potencial TOTAL gerado em tenha o triplo do valor daquele gerado unicamente pelo bastão.

Um bastão cilíndrico isolante, de comprimento muito longo e raio (com ), foi carregado com uma densidade volumétrica de carga não uniforme , onde é uma constante. A carga total no bastão é .

O bastão está envolvido por uma casca cilíndrica condutora concêntrica de mesma altura e de raios e , conforme mostra a Figura. A configuração se encontra em condições de equilíbrio eletrostático.

O campo elétrico gerado a uma distância () do eixo de simetria comum é igual a e a carga total na superfície externa (raio ) da casca condutora é .

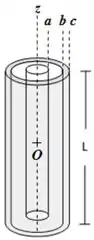
(a) Expresse em função de e do volume do bastão.

(b) Calcule as densidades superficiais de carga e nas superfícies interna e externa da casca condutora, respectivamente. No cálculo de , expresse em função de e da área da superfície externa da casca condutora.

(c) Obtenha o valor (módulo) do campo elétrico em um ponto arbitrário do interior do bastão () e muito afastado de suas extremidades.

(d) Obtenha o valor (módulo) do campo elétrico em um ponto arbitrário situado entre o bastão e a superfície interna da casca condutora () e muito afastado de suas extremidades.

(e) Obtenha o valor (módulo) do campo elétrico em um ponto arbitrário do interior da casca condutora () e muito afastado de suas extremidades.

(f) Obtenha o valor (módulo) do campo elétrico em um ponto arbitrário do exterior da casca condutora () e muito afastado de suas extremidades.