P1 de Física 3 - FIS1051 da PUCRIO - 2017.2

Uma esfera de raio possui uma distribuição de carga não uniforme cuja densidade volumétrica é igual a , onde é uma constante positiva com dimensões: .

Calcule, utilizando explicitamente a Lei de Gauss:

O campo elétrico no ponto , a uma distância do centro da esfera.

O campo elétrico no ponto , a uma distância do centro da esfera.

A diferença de potencial entre os pontos e .

Suponha agora que uma carga puntiforme com massa e velocidade se desloque do infinito até o centro da esfera.

Calcule a distância mínima alcançada pela carga antes de ser repelida pela esfera.

(Sugestão: calcule o potencial da esfera numa distância genérica e utilize a conservação da energia).

Considere um bastão (muito fino) isolante de comprimento carregado com uma densidade de carga uniforme . O bastão está orientado na direção horizontal.

Desenhe o bastão e o sistema de coordenadas utilizado.

Calcule agora o campo elétrico (módulo, direção e sentido) nos seguintes pontos:

Em um ponto qualquer numa altura acima do bastão.

Em um ponto numa altura acima do centro do bastão.

Se agora o bastão tem comprimento infinito, como se modifica a resposta do item ?

Considere a casca esférica isolante representada na figura abaixo.

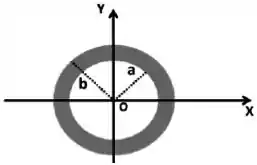
O centro da casca esférica coincide com as origens dos eixos . O raio interno da casca é , aquele externo . A densidade volumétrica de carga NÃO é uniforme e tem a seguinte expressão:

Calcule as unidades de medida da constante .

Calcule o potencial elétrico na origem dos eixos.

Calcule o campo elétrico na origem dos eixos, SEM utilizar a Lei de Gauss.

Suponha agora que a carga liquida da casca esférica se conserve, mas que o material isolante seja trocado por um material condutor. Seja o valor da carga líquida (conhecido).

Calcule, em função de , o valor das densidades superficiais de cargas e (interna e externa) da casca esférica.

O potencial elétrico na origem dos eixos muda de valor em comparação ao valor calculado no item ? Se não mudar, justifique porquê. Se mudar, calcule o novo valor em função de , usando o método que preferir.