Três cargas puntiformes de igual valor e idênticas massas , são penduradas de um ponto comum por fios isolantes, todos de comprimento . Na situação de equilíbrio, o arranjo fica como ilustrado na Figura ao lado (considere a aceleração da gravidade conhecida).
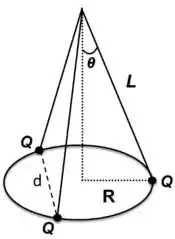
a) Calcule a distância, , de equilíbrio entre as cargas em função de (veja o desenho).
b) Calcule o valor da força elétrica resultante sobre cada uma das cargas devido à ação das demais. Expresse seu resultado em termos do ângulo e do comprimento .
c) Calcule o valor de cada carga em função de , e (Sugestão: lembre-se que no equilíbrio a força total resultante nas cargas deve ser igual a zero).
Passo 1
Como todas as cargas são iguais, temos que a distância entre elas deve ser a mesma, ou seja, as cargas estão dispostas nos vértices de um triângulo equilátero. Esse triângulo equilátero está circunscrito em um círculo de raio .
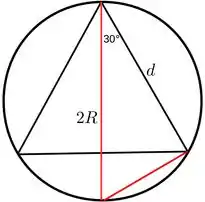
Temos um triângulo retângulo cuja hipotenusa é e o cateto adjacente ao ângulo de é . Assim
Passo 2
Vamos olhar para a carga da ponta de cima.
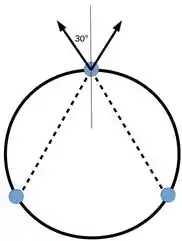
Nessa carga, vemos que só haverá força na direção vertical. Como as outras duas cargas estão a mesma distância da carga que estamos olhando, temos que a força que cada uma exerce é
Para pegar a componente vertical dessa força, multiplicamos pelo cosseno de . Como a força total é duas vezes essa força vertical, temos que
Porém nossa resposta tem que estar em termos de e . Isso é feito reparando na primeira figura
Assim
Passo 3
Agora temos que usar a condição de que o sistema está em equilíbrio. Isso quer dizer que as forças no plano do círculo se anulam e fora do plano também
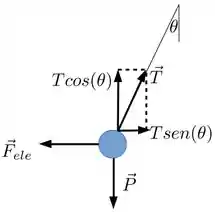
onde é a força devido às outras duas cargas. Assim temos duas equações
Dividindo uma pela outra, teremos