Um bastão cilíndrico isolante, de comprimento muito longo e raio (com ), foi carregado com uma densidade volumétrica de carga não uniforme , onde é uma constante. A carga total no bastão é .
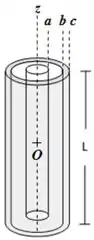
O bastão está envolvido por uma casca cilíndrica condutora concêntrica de mesma altura e de raios e , conforme mostra a Figura. A configuração se encontra em condições de equilíbrio eletrostático.
O campo elétrico gerado a uma distância () do eixo de simetria comum é igual a e a carga total na superfície externa (raio ) da casca condutora é .
(a) Expresse em função de e do volume do bastão.
(b) Calcule as densidades superficiais de carga e nas superfícies interna e externa da casca condutora, respectivamente. No cálculo de , expresse em função de e da área da superfície externa da casca condutora.
(c) Obtenha o valor (módulo) do campo elétrico em um ponto arbitrário do interior do bastão () e muito afastado de suas extremidades.
(d) Obtenha o valor (módulo) do campo elétrico em um ponto arbitrário situado entre o bastão e a superfície interna da casca condutora () e muito afastado de suas extremidades.
(e) Obtenha o valor (módulo) do campo elétrico em um ponto arbitrário do interior da casca condutora () e muito afastado de suas extremidades.
(f) Obtenha o valor (módulo) do campo elétrico em um ponto arbitrário do exterior da casca condutora () e muito afastado de suas extremidades.
Passo 1
Podemos relacionar a densidade volumétrica de carga do bastão com a sua carga total por
onde usaremos coordenadas cilíndricas e
Assim a integral de volume ficará
O volume desse cilindro é
Passo 2
Temos que, dentro do condutor, o campo elétrico deve ser nulo.
Se escolhermos uma superfície gaussiana cilíndrica cuja área lateral está dentro do condutor (com raio ), temos que o fluxo do campo elétrico ao longo dessa superfície tem que ser nulo.
Pela lei de Gauss
vemos que a carga total dentro dessa superfície tem que ser nula.
Como já temos uma carga no bastão interno, temos que ter uma carga distribuída na superfície interna. Dessa forma a densidade superficial de carga nessa interface será
Como a área da superfície interna é
Então
Passo 3
Como na casca externa temos uma carga , a densidade de carga na superfície externa é dada por
onde é a área da superfície externa.
Só temos um problema aqui: o enunciado pediu para relacionarmos com o campo gerado a uma distância !
Passo 4
Vamos de novo recorrer a lei de Gauss!
Agora vamos escolher uma superfície gaussiana cilíndrica de raio ( e altura bem menor que a altura . A carga total dentro dessa superfície será
onde o segundo termo é a carga na casca interna e o terceiro é a carga no bastão. Como um anula o outro só sobra a carga na casca externa!
Agora temos que sabe o fluxo através dessa superfície. Como o campo é radial, só haverá fluxo através da área lateral desse cilindro. Assim como o campo a uma distância é
Agora usando a lei de Gauss
Para deixar tudo redondo, temos que lembrar que a área lateral da superfície é , de forma que
Agora podemos voltar para densidade superficial de carga!
Passo 5
Agora temos que usar a lei de Gauss usando uma superfície cilíndrica de raio e altura .
O fluxo do campo elétrico será
A carga total dentro dessa superfície será
lembrando que
Agora aplicando a lei de Gauss
Passo 6
Agora temos que usar a lei de Gauss usando uma superfície cilíndrica de raio e altura .
O fluxo do campo elétrico será
A carga total dentro dessa superfície será
(a diferença do passo anterior é que agora estamos contando a carga toda no bastão e não só em um cilindro de raio )
lembrando que
Agora aplicando a lei de Gauss
Passo 7
Essa parte aqui é a molezinha pra respirar! A região é dentro do condutor, ou seja, o campo aqui é nulo!
Passo 8
Agora vamo que vamo!!! Última região para calcular o campo elétrico!!!! \o/
Agora temos que usar a lei de Gauss usando uma superfície cilíndrica de raio e altura .
O fluxo do campo elétrico será
Agora para contar a carga total dentro dessa superfície vamos só considerar a carga da casca externa (. Isso por que a carga distribuída na casca interna está blindando a o campo vindo do bastão.
Como a densidade de carga na casca externa é
Agora aplicando a lei de Gauss
Mas já calcularmos
Assim o campo fica