Considere um bastão (muito fino) isolante de comprimento carregado com uma densidade de carga uniforme . O bastão está orientado na direção horizontal.
Desenhe o bastão e o sistema de coordenadas utilizado.
Calcule agora o campo elétrico (módulo, direção e sentido) nos seguintes pontos:
Em um ponto qualquer numa altura acima do bastão.
Em um ponto numa altura acima do centro do bastão.
Se agora o bastão tem comprimento infinito, como se modifica a resposta do item ?
Passo 1
Desenhe o bastão e o sistema de coordenadas utilizado.
Então vambora! O que temos que fazer aqui é determinar onde vamos colocar o bastão carregado em relação ao sistema de coordenadas. Então a boa aqui é encontrar um arranjo que não complique tanto a nossa vida.
Como o bastão carregado está na horizontal, vamos assumir aqui que o plano é o plano horizontal (com o eixo perpendicular ao plano da tela) e vamos posicionar esse bastão ao longo do eixo .
No entanto, na letra vamos ter que calcular o campo elétrico em um ponto qualquer acima da barra. Então, como estamos sempre com a cabeça à frente do nosso tempo, não vamos colocar o bastão simétrico em relação ao eixo , se liga:
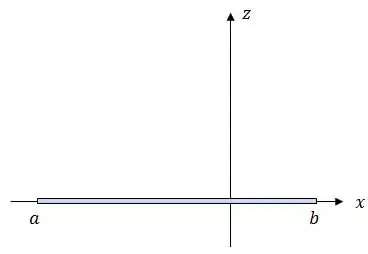
Onde , que é o comprimento do bastão.
“Tá! Mas eu poderia colocar o bastão simétrico em relação ao eixo ?!”
Parceiro! Aqui é você quem manda! Mas vamos ver no próximo passo que utilizar essa configuração vai nos ajudar.
Passo 2
Calcule agora o campo elétrico (módulo, direção e sentido) em um ponto qualquer numa altura acima do bastão.
Ok, vamos começar posicionando o nosso ponto . Como os pontos e que limitam o bastão são pontos genéricos, podemos posicionar o ponto sobre o eixo .
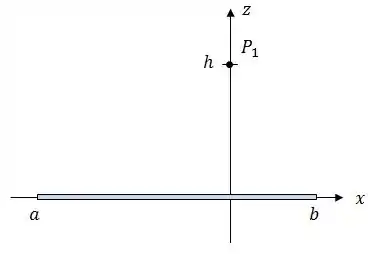
“Ok! Qual é a estratégia agora?”
Pra esse tipo de problema, nós começamos olhando pra um pedaço infinitesimal desse bastão, com carga e posicionado em um ponto qualquer.
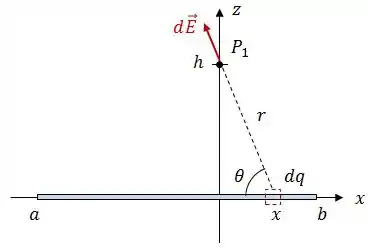
O módulo do campo elétrico infinitesimal gerado por esse pedaço do fio é dado por:
Passo 3
O próximo passo é encontrar as componentes em e em desse campo elétrico. Pra isso, vamos utilizar o ângulo que apareceu na última imagem.
Além disso, repare que a componente em do campo elétrico aponta no sentido negativo do eixo , enquanto a componente em do campo elétrico aponta no sentido positivo do eixo , logo:
Dessa forma:
Onde:
Substituindo nas expressões dos campos elétricos, teremos:
Passo 4
Pra fechar, basta integrar as expressões de campo elétrico que encontramos, onde . Se liga:
Ok! Sei que essas integrais podem assustar, mas o formulário da prova já nos dá a resposta pra esses caras!
Segundo o formulário:
Agora é só substituir os limites de integração e ser feliz!
Passo 5
Calcule o campo elétrico em um ponto numa altura acima do centro do bastão.
Como agora estamos interessados em um ponto acima do centro do bastão, podemos reorganizar o nosso sistema da seguinte forma:
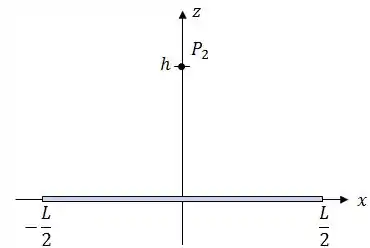
“Beleza, mas o que isso muda em relação ao que fizemos até agora?!”
A diferença é que agora sabemos quem são os nossos pontos e !
Como agora o bastão está simétrico em relação ao eixo :
“E agora?”
Agora é só substituir nas expressões de e , se liga:
Passo 6
Se agora o bastão tem comprimento infinito, como se modifica a resposta do item ?
Pra analisar melhor a situação, vamos utilizar a expressão que encontramos na letra para o campo elétrico :
Se a barra for infinita, significa que , logo:
Sendo assim:
Resposta