Considere a casca esférica isolante representada na figura abaixo.
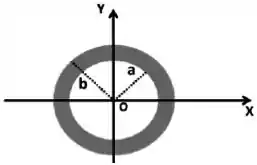
O centro da casca esférica coincide com as origens dos eixos . O raio interno da casca é , aquele externo . A densidade volumétrica de carga NÃO é uniforme e tem a seguinte expressão:
Calcule as unidades de medida da constante .
Calcule o potencial elétrico na origem dos eixos.
Calcule o campo elétrico na origem dos eixos, SEM utilizar a Lei de Gauss.
Suponha agora que a carga liquida da casca esférica se conserve, mas que o material isolante seja trocado por um material condutor. Seja o valor da carga líquida (conhecido).
Calcule, em função de , o valor das densidades superficiais de cargas e (interna e externa) da casca esférica.
O potencial elétrico na origem dos eixos muda de valor em comparação ao valor calculado no item ? Se não mudar, justifique porquê. Se mudar, calcule o novo valor em função de , usando o método que preferir.
Passo 1
Calcule as unidades de medida da constante .
De acordo com o enunciado, a densidade volumétrica de carga, para , é dada por:
Pra calcular as unidades de medida de , basta fazer uma análise dimensional da expressão acima:
Onde:
Logo:
Passo 2
Calcule o potencial elétrico na origem dos eixos.
Como o problema já nos avisou que não podemos utilizar a Lei de Gauss, teremos que ir por outro caminho.
Vamos dividir então essa casca esférica em várias cascas esféricas de espessura infinitesimal, com uma carga , de forma que o potencial gerado, na origem, por cada casca é dada por:
Onde podemos associar a carga à densidade volumétrica de carga da seguinte forma:
Onde , e .
Substituindo na expressão do potencial, teremos:
Agora é só integrar esse cara:
Finalmente:
Passo 3
Calcule o campo elétrico na origem dos eixos, SEM utilizar a Lei de Gauss.
Aquele momento em que o problema te pede pra calcular o campo elétrico sem usar a Lei de Gauss:

Mas relaxa! Essa é uma questão meramente argumentativa.
Se liga! Se pegarmos dois pontos simetricamente opostos com uma carga infinitesimal , o campo elétrico gerado por esses dois caras, no centro, vai ser dado da seguinte forma:
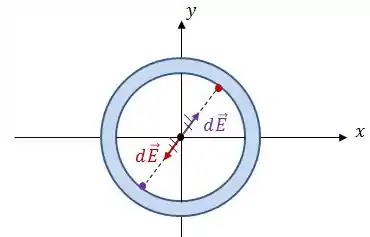
Ou seja, por conta da forma como a carga está distribuída na casca esférica (variando apenas com o raio), todos os pares de pontos simetricamente opostos gerarão campos elétricos que se cancelam na origem.
Como resultado, o campo elétrico na origem será nulo.
Passo 4
Calcule, em função de , o valor das densidades superficiais de cargas e (interna e externa) da casca esférica.
Ao trocarmos o material da casca esférica para um condutor, como não há nenhuma carga na cavidade, toda a carga agora irá se acumular na superfície externa, logo:
Dessa forma, as densidades de cargas nas superfícies serão:
Passo 5
O potencial elétrico na origem dos eixos muda de valor em comparação ao valor calculado no item ? Se não mudar, justifique porquê. Se mudar, calcule o novo valor em função de , usando o método que preferir.
Para calcular o potencial na origem, vamos utilizar a seguinte equação:
Sendo assim, vamos começar encontrando uma expressão para o campo elétrico.
Utilizando a Lei de Gauss nesta situação, dada a simetria esférica, teremos::
No entanto, para qualquer valor de não há carga no interior da superfície gaussiana. Isso significa que, nesse caso:
Para a gaussiana engloba a superfície externa da casca esférica, com carga , logo:
Passo 6
Agora estamos prontos pra calcular o potencial elétrico na origem!

Para isso, vamos aplicar a equação da ddp aplicada a duas regiões: e , usando como ponto inicial o infinito (onde o potencial é nulo). Dessa forma:
Substituindo as expressões para essas regiões que encontramos no Passo 5, e lembrando que teremos:
Resposta
.