P1 de Física 3 - FIS1051 da PUCRIO - 2019.1

Um fio de comprimento (com extremidades localizadas nos pontos e do eixo ) está carregado com uma densidade de carga uniforme . Todos os pontos de interesse para o problema estão localizados no plano ().

1. Calcule o campo elétrico gerado pelo fio carregado em pontos do eixo , para e para .
2. Calcule o potencial elétrico gerado pelo fio carregado em pontos do eixo , para e para .
3. Encontre o valor do campo elétrico no ponto para .

Uma partícula de carga e massa é então colocada em com velocidade inicial nula. Ela se move apenas sob a ação da força eletrostática repulsiva devido ao fio. Ignore efeitos gravitacionais.

4. Calcule a aceleração da partícula quando ela está em alguma posição .
5. Calcule a velocidade final da partícula carregada quando ela está a uma distância muito grande do fio.

Três cargas pontuais ocupam vértices de um quadrado de lado , conforme a figura. Dois vértices opostos são ocupados por cargas iguais a e o terceiro é ocupado pela carga . Adote o infinito como referencial para potenciais nulos.

1. Calcule em função de de modo que o potencial resultante no quarto vértice seja nulo.
2. Considerando agora , calcule a energia potencial elétrica associada ao sistema de três cargas.
3. Considerando sempre , calcule a variação de energia potencial elétrica ao movermos uma das cargas desde o vértice em que está até o quarto vértice do quadrado.

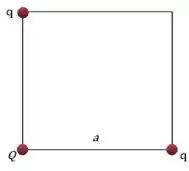
Considere uma casca cilíndrica isolante de altura “infinita”, raio interno e raio externo . Ao longo desse cilindro existe uma carga distribuída homogeneamente com densidade volumétrica não uniforme .

Nota: a figura mostra a seção transversal da casca cilíndrica.

a) Encontre o módulo do campo elétrico na região .

b) Encontre o módulo do campo elétrico fora da casca .

c) Encontre o módulo do campo elétrico dentro da casca, .

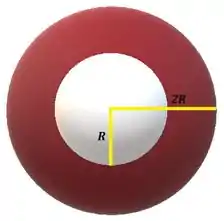
Considere agora que a casca cilíndrica seja envolvida por uma outra casca cilíndrica condutora de raio interno e raio externo . A carga líquida da casca condutora é nula e o sistema já alcançou o equilíbrio eletrostático.

d) Encontre o módulo do campo elétrico na região .

e) Encontre o módulo do campo elétrico na região .

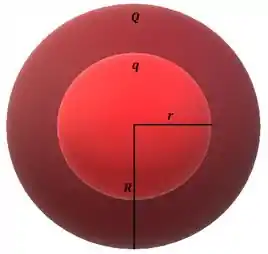
Entre as duas cascas esféricas delgadas condutoras concêntricas da figura não há nenhum contato elétrico. A casca interna possui raio e carga e a casca externa possui raio e carga . Considerando o referencial para potenciais nulos no infinito, sabe-se que o potencial na casca maior vale e na casca menor vale .

d) Calcule em função de , , , e da constante de Coulomb .