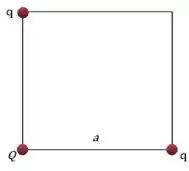
Três cargas pontuais ocupam vértices de um quadrado de lado , conforme a figura. Dois vértices opostos são ocupados por cargas iguais a e o terceiro é ocupado pela carga . Adote o infinito como referencial para potenciais nulos.
- Calcule em função de de modo que o potencial resultante no quarto vértice seja nulo.
- Considerando agora , calcule a energia potencial elétrica associada ao sistema de três cargas.
- Considerando sempre , calcule a variação de energia potencial elétrica ao movermos uma das cargas desde o vértice em que está até o quarto vértice do quadrado.
Passo 1
a)Ta, antes de qualquer coisa, vamos lembrar a fórmula do potencial
Onde vai ser a distância da carga até o quarto vértice.
No caso desse exercício, temos mais de 2 cargas, então o potencial resultante no quarto vértice vai ser
Passo 2
O enunciado pede pro nosso potencial resultante ser 0 e também quer que a gente escreva em função de , então:
Passo 3
b) A energia potencial elétrica é calculada assim
Maaas, novamente, como é um sistema de 2 cargas, ela vai ficar assim
Passo 4
c)Vamos escolher a carga da aresta de baixo pra ser a carga que vai se mover ok? Mas poderia ser a outra também!! Quando essa carga se mover, a variação de energia potencial elétrica vai ser