P1 de Física 3 - FIS1051 da PUCRIO - 2020.2

Um arame circular horizontal, de raio R, contém três contas carregadas em equilíbrio, de cargas Q, Q e q, como mostra a Figura 2. As distâncias entre as contas de carga Q e a de carga q é dada por L, enquanto a distância entre as duas contas de carga Q é dada por D, formando um triângulo isósceles. As contas só podem se mover, sem atrito, ao longo do arame circular.

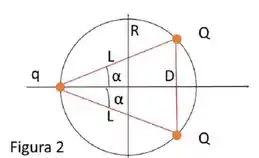
d) Expresse a energia potencial eletrostática total do sistema de três cargas, U, como função de {q, Q, α, R}.

e) Suponha que q = Q. Obtenha o valor de α que minimiza a energia eletrostática total do sistema U.

Dois pedaços de fios retos semi-infinitos, isolantes e carregados (densidades de carga λ e – λ) estão colados a dois semicírculos de raio R formados de fios isolantes carregados (densidades de carga 2λ e - λ), como mostra a Figura 1.

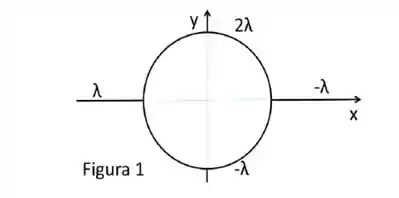
a) Calcule o vetor campo elétrico na origem das coordenadas devido aos fios semi-infinitos retos.

b) Calcule o vetor campo elétrico na origem das coordenadas devido aos fios semicirculares.

c) Calcule o campo eletrostático vetorial total na origem das coordenadas.

Uma meia coroa circular isolante de espessura desprezível (veja a figura abaixo), com raio interno e raio externo , está carregada com uma carga total Q > 0. A densidade superficial de carga não é uniforme e vale , onde é uma constante positiva e é a distância do centro da coroa até qualquer ponto sobre ela.

Considere o potencial nulo no infinito.

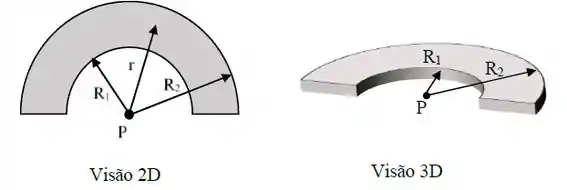
a) Determine a expressão para a carga total Q na meia coroa em função dee.

b)Obtenha uma expressão para o potencial elétrico no ponto P situado no centro da meia coroa, em função de e.

c) Considere agora uma aproximação em que o raio interno se iguale ao raio externo (a meia coroa circular se transforma em um meio anel). Neste caso, vamos considerar uma densidade linear de carga uniforme e igual a . Calcule, nesta condição:

i) a carga total Q do meio anel;

ii) a expressão para o potencial elétrico no ponto P no centro do anel.

d)Calcule o trabalho que deve ser realizado por um agente externo para transportar uma carga do infinito até o ponto P.

Uma esfera sólida isolante carregada de raio R é envolvida por uma casca esférica condutora de raio interno e raio externo e carga líquida nula. As cargas da esfera isolante estão distribuídas de forma esfericamente simétrica com densidade volumétrica de cargas , onde r é à distância com relação ao centro da esfera.

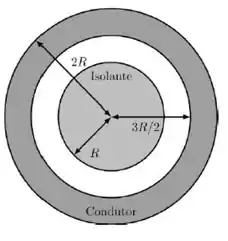
a) Se considerarmos que , qual deve ser o valor de α para que o campo elétrico a uma distância do centro da configuração seja nulo? Em outras palavras, E(4R/3) = 0.

Para os próximos itens considere que . Utilizando a Lei de Gauss, encontre a magnitude do campo elétrico E(r) nas regiões:

b) r

c) R

d)3R/2

e)2R

Considere, apenas para o item (f), que e.

f) Calcule a densidade superficial de carga σ da superfície externa da casca condutora.