Uma meia coroa circular isolante de espessura desprezível (veja a figura abaixo), com raio interno e raio externo , está carregada com uma carga total Q > 0. A densidade superficial de carga não é uniforme e vale , onde é uma constante positiva e é a distância do centro da coroa até qualquer ponto sobre ela.
Considere o potencial nulo no infinito.
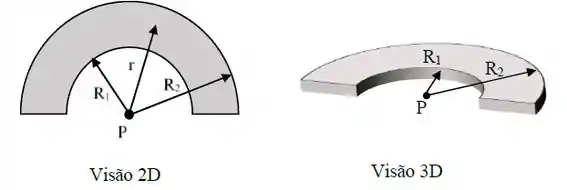
a) Determine a expressão para a carga total Q na meia coroa em função dee.
b)Obtenha uma expressão para o potencial elétrico no ponto P situado no centro da meia coroa, em função de e.
c) Considere agora uma aproximação em que o raio interno se iguale ao raio externo (a meia coroa circular se transforma em um meio anel). Neste caso, vamos considerar uma densidade linear de carga uniforme e igual a . Calcule, nesta condição:
i) a carga total Q do meio anel;
ii) a expressão para o potencial elétrico no ponto P no centro do anel.
d)Calcule o trabalho que deve ser realizado por um agente externo para transportar uma carga do infinito até o ponto P.
Passo 1
Fala galera, tudo bem? Essa questão parece complicada, mas vou ajudar você!
Letra (a):
Temos uma quantidade de carga distribuída em um semi anel, então precisamos integrar sobre toda superfície para achar o valor da carga total.
A densidade superficial é a divisão da carga total pela área, então temos:
Os limites de integração são:
Juntando tudo em uma integral teremos:
A densidade é independente do ângulo, então essa integral podemos resolver:
Beleza até aqui?
Passo 2
Letra (b):
O diferencial de potencial é:
O diferencial de carga é:
E juntando tudo isso temos:
Passo 3
Letra (c):
- Quando temos um fio, a densidade é linear e tem valor de . O diferencial de comprimento no ponto que é , e temos que . O diferencial de carga é . Agora é só integrar para determinar a carga total:
- Agora a distância do ponto até o fio é constante e vale . Assim o potencial é:
Passo 4
Letra (d):
O trabalho vai ser a variação da energia potencial:
Espero ter ajudado!