PUCRIO – Física 3 2020.2 – P1 – Questão 1B
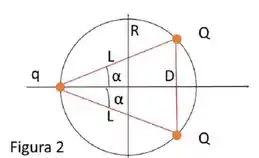
Um arame circular horizontal, de raio R, contém três contas carregadas em equilíbrio, de cargas Q, Q e q, como mostra a Figura 2. As distâncias entre as contas de carga Q e a de carga q é dada por L, enquanto a distância entre as duas contas de carga Q é dada por D, formando um triângulo isósceles. As contas só podem se mover, sem atrito, ao longo do arame circular.
d) Expresse a energia potencial eletrostática total do sistema de três cargas, U, como função de {q, Q, α, R}.
e) Suponha que q = Q. Obtenha o valor de α que minimiza a energia eletrostática total do sistema U.
Passo 1
Fala galera, tudo bem? Essa questão parece complicada, mas vou ajudar você!
Letra (d):
Temos três cargas, então temos três pares para contabilizar na energia. Precisamos contabilizar a energia de trazer as três cargas do infinito até aqui. Então temos:
Certo?
Beleza até aqui?
O problema ficou determinar as distâncias e em termos do raio e do ângulo .
Passo 2
Olhando o triângulo , o ângulo interno é e podemos aplicar a lei dos cossenos para determinar em função de e .
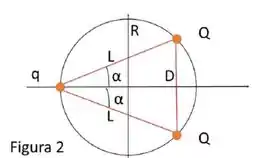
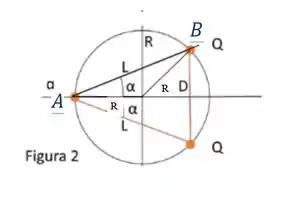
Da lei dos cossenos temos:
E analisando o triângulo temos que é igual a . Daí temos:
Aí a energia potencial desse sistema é:
Ou melhor:
Passo 3
Letra (e): para a energia fica assim:
E o valor de que minimiza é quando temos , então precisamos derivar essa coisinha aí:
E daí temos:
Espero ter ajudado!