Dois pedaços de fios retos semi-infinitos, isolantes e carregados (densidades de carga λ e – λ) estão colados a dois semicírculos de raio R formados de fios isolantes carregados (densidades de carga 2λ e - λ), como mostra a Figura 1.
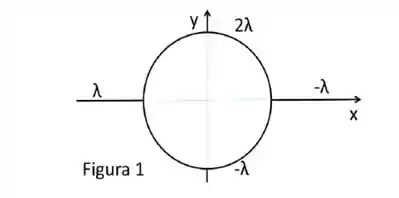
a) Calcule o vetor campo elétrico na origem das coordenadas devido aos fios semi-infinitos retos.
b) Calcule o vetor campo elétrico na origem das coordenadas devido aos fios semicirculares.
c) Calcule o campo eletrostático vetorial total na origem das coordenadas.
Passo 1
Fala galera, tudo bem? Essa questão parece complicada, mas vou ajudar você!
Letra (a):
A idéia pra resolver essas questões de campo em um fio é primeiro sempre olhar a simetria e ver pra onde o campo vai apontar. Depois escrever o diferencial de carga e os limites de integração, juntar tudo e integrar! Vamos lá?
Sabemos que no centro o fio semi infinito reto mais à esquerda produz um campo horizontal para a direita, certo? E o outro fio, o mais à direita? Também! Ele tem densidade de carga negativa, então o campo produzido por ele vai ser “entrando”, que é na direção também. Então vou calcular para um fio e multiplicar por dois, ok?
Agora o diferencial de carga. Como temos uma distribuição uniforme, um pedacinho do fio vai ter um pedacinho de cargas:
Agora os limites. Vou olhar o fio da esquerda. Você pode tentar o outro lado e verificar que dá o mesmo resultado =) A distância até o ponto vamos dizer que é , e o mais próximo que ela chega do ponto é quando , e o mais longe? Como o fio é semi infinito, o mais longe que pode chegar é , então os limites são:
Aí o diferencial de campo fica:
Agora é só integrar tudo:
E aí o campo vetorial dos dois fios vai ser:
Beleza até aqui?
Passo 2
Letra (b):
Agora vou analisar os semicírculos. O semicírculo superior produz um campo para baixo por simetria, já que a densidade de cargas é positiva. E o semicírculo inferior? Ele também produz um campo para baixo! Já que sua densidade é negativa! Então vou começar calculando o campo do fio superior.
O diferencial de cargas para um fio circular é:
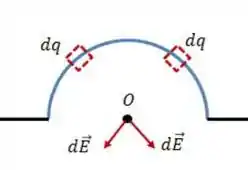
E o campo é proporcional ao seno desse ângulo, por simetria, daí o campo fica assim:
E juntando tudo isso e integrando teremos:
Para o semicírculo inferior a única diferença é a densidade de carga que é a metade da do fio superior, então o campo elétrico do fio inferior vai ser metade do campo do fio superior:
E a direção é vertical para baixo então o campo vetorial total dos fios é dado por:
Passo 3
Letra (c):
E agora o campo vetorial total vai ser a soma de todos os campos. Juntando as respostas dos itens anteriores temos:
Espero ter ajudado!