P3 de Física 3 - FIS1051 da PUCRIO - 2012.2

Considere que no circuito abaixo temos , e . Sabendo que a fonte opera com frequência angular de e com uma tensão eficaz (valor quadrático médio) de , determine:

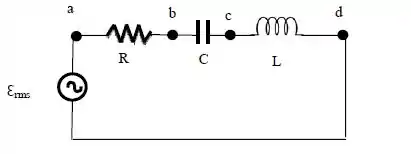
O valor eficaz (quadrático médio) da corrente no circuito.

As tensões eficazes , , , e . (Faça o diagrama de fasores para ajudar no raciocínio).

A potência média fornecida pela fonte e a potência média dissipada em cada elemento do circuito.

O ângulo de fase entre a tensão da fonte e a corrente se a frequência angular mudar para . Neste caso quem está adiantado, a corrente ou a tensão da fonte?

Uma espira condutora retangular de superfície e resistência gira ao redor do eixo com velocidade angular constante num campo magnético uniforme de modulo B e direção e sentido ao longo do eixo como mostrado na figura ao lado.

Considere o sentido do vetor unitário característico da superfície da espira para efeito de fluxo magnético como mostrado em figura.

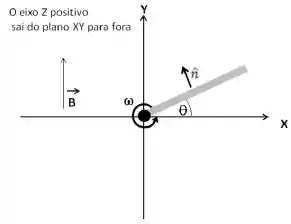
Determine o sinal do fluxo magnético que atravessa a espira e da sua derivada temporal nos seguintes intervalos:

Determine a expressão do fluxo magnético que atravessa a espira e da induzida em função do ângulo . Faça um gráfico das duas grandezas para .

Calcule a potencia elétrica dissipada no resistor em função do ângulo .

Qual deve ser a potência em função de tempo de um motor que está forçando a espira a girar com uma velocidade ? A potência média durante uma volta completa da espira é menor, maior ou igual a potencia elétrica dissipada no resistor? Justifique através de considerações energéticas.

Sugestão: A potência é igual ao momento τ aplicado pelo motor vezes a velocidade angular .

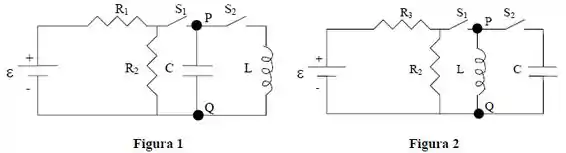
Considere o circuito da figura 1 onde , , , , e ocorrem as seguintes fases sucessivas:

Fase1: chave fechada e aberta durante longo tempo

Fase 2: chave aberta e fechada durante longo tempo

Determine, justificando todas as respostas:

A ddp em função do tempo durante a fase 2.

A corrente no indutor em função do tempo durante a fase 2.

A carga do capacitor em função do tempo durante a fase 2.

A energia do circuito durante a fase 2.

Considere agora que as posições do indutor e do capacitor são trocadas e a resistência é substituída por outra , conforme a Figura 2. Nestas novas condições, determine:

O valor da resistência tal que a energia do circuito seja igual ao da Figura 1.

Se o indutor no circuito da Figura 1 tem uma resistência interna , após quanto tempo a energia inicial do circuito decai de , sendo “ a base dos logaritmos naturais.