Considere que no circuito abaixo temos , e . Sabendo que a fonte opera com frequência angular de e com uma tensão eficaz (valor quadrático médio) de , determine:
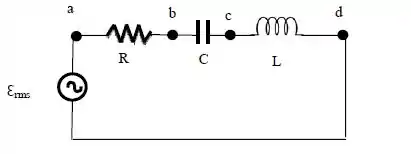
O valor eficaz (quadrático médio) da corrente no circuito.
As tensões eficazes , , , e . (Faça o diagrama de fasores para ajudar no raciocínio).
A potência média fornecida pela fonte e a potência média dissipada em cada elemento do circuito.
O ângulo de fase entre a tensão da fonte e a corrente se a frequência angular mudar para . Neste caso quem está adiantado, a corrente ou a tensão da fonte?
Passo 1
O valor eficaz (quadrático médio) da corrente no circuito.
O valor eficaz da corrente é dada por:
Onde:
Voltando...
Passo 2
As tensões eficazes , , , e . (Faça o diagrama de fasores para ajudar no raciocínio).
Passo 3
A potência média fornecida pela fonte e a potência média dissipada em cada elemento do circuito.
A potência média fornecida ao circuito é dada por:
Ou:
Onde:
Logo:
A potência dissipada em cada elemento será dada por:
O capacitor e o indutor não dissipam energia, logo:
Passo 4
O ângulo de fase entre a tensão da fonte e a corrente se a frequência angular mudar para . Neste caso quem está adiantado, a corrente ou a tensão da fonte?
Se a frequência mudar, os valores das reatâncias capacitiva e indutiva serão:
Como , essa frequência corresponde à frequência de ressonância. Assim, o ângulo de fase será:
Logo, a tensão e a fonte estão em fase.
Resposta
Logo, a tensão e a fonte estão em fase.